răspunsuri la întrebări de testare;
Concluziile lucrări practice.
1.2. Prezentare generală
Una dintre etapele cele mai intensiv forța de muncă de rezolvare a problemei pe un computer este de a dezvolta un algoritm.
Prin algoritm se înțelege prescrierea exactă, definind un proces de calcul, ceea ce duce prin varierea datele inițiale la rezultatul dorit.
Principalele caracteristici caracteristice ale algoritmului sunt:
determinism (certitudine) - cu datele inițiale furnizate de unicitatea rezultatului dorit;
masa - adecvare pentru acest tip de sarcină, atunci când datele inițiale care aparțin unui anumit subset;
eficacitate - pus în aplicare printr-un procedeu de calcul se realizează într-un număr finit de pași cu emiterea unui rezultat semnificativ;
discret - posibilitatea de a algoritmului de divizare în etape separate, punerea în aplicare a care nu este pusă la îndoială.
Următoarele tipuri de procese de calcul:
proces de calcul liniar.
Pentru a obține rezultatul care aveți nevoie pentru a efectua unele operațiuni în ordine.
Ramificat proces de calcul.
Secvența particulară a operațiilor depinde de valorile unuia sau mai multor parametri. De exemplu, dacă discriminantul ecuației pătratice nu este negativ, atunci ecuația are două rădăcini, iar dacă este negativ, atunci nu există nici rădăcini reale.
proces de calcul ciclica
Pentru a obține rezultatul unei secvențe de etape trebuie să fie efectuate de mai multe ori. De exemplu, în scopul de a obține un tabel de valori ale unui interval predeterminat de argument, cu un pas predeterminat, numărul de ori necesar pentru a determina valoarea următoare a argumentului, și se calculează funcția sa de valoare.
La rândul său, există, de asemenea, mai multe tipuri de calcul a procesului ciclic. și anume:
cicluri de numarare (cicluri numărul predeterminat de repetiții) - - o procese ciclice pentru care se cunoaște numărul de repetiții.
cicluri iterative - un proces ciclic, care se termină la atingerea sau încălcarea anumitor condiții.
Ciclul de căutare - un proces ciclic, din care există două opțiuni de ieșire:
- randament finalizarea procesului;
- pensionare anticipată pentru orice condiție suplimentară.
În funcție de tipul de calcul algoritm proces pus în aplicare, se disting:
- Structura algoritmilor liniare;
- Algoritmi structuri ramificate;
- algoritmi de structură ciclică.
Algoritmi pentru rezolvarea problemelor practice au de obicei o structură combinată, adică, să includă toate cele trei tipuri de procese de calcul.
Prin descrierea vizuală a algoritmilor includ următoarele metode principale de prezentare a acestora:
- verbale (în intrările în limbaj natural);
- structurale și stilizată (înregistrarea pe limba algoritmică și pseudo-cod);
- (modelele de imagini și simboluri grafice) grafice;
- Software (texte în limbaje de programare).
Descrierea verbală a metodei a algoritmului este o descriere a datelor succesive etape numerotate și este dat în mod arbitrar prezentarea limbajului natural.
Algoritmul de a adăuga două numere (a și b).
Întrebați, ceea ce este numărul unui.
Întrebați, ceea ce este numărul de b.
Ori a și b, cu assign rezultat.
Raport rezultatul a.
Avantajul acestei metode este simplitatea descrierii și dezavantajul este că această abordare este prolix și nu are nici o formalizare strictă, astfel permite interpretarea ambiguă a anumitor cerințe, prin care o metodă algoritm de reprezentare verbală nu este larg răspândită.
Pentru algoritmi de prelucrare a datelor de setare diverse stricte și structurile lor trebuie să aibă un sistem formal de simboluri și reguli folosite pentru a sesiza orice dispoziții interpretate cu precizie și fără ambiguități. Normele relevante ale sistemului este descrierile lingvistice. Acestea includ limbaje algoritmice (pseudo-cod), scheme logice și limbaje de programare.
mod de a descrie un algoritm bazat pe înregistrarea algoritmilor în regulamentele de reprezentare a unei formalizate definite prin utilizarea unui set limitat de construcții sintactice standard, de multe ori numite pseudo-cod Structural-stilizate.
Avantajul este apropierea de limbajele de programare pseudo-cod și dezavantajele, la rândul lor, sunt complexitatea dezvoltării și imposibilitatea de intrare directă a algoritmului de rezolvare a unui calculator, și anume, necesitatea de a traduce un limbaj de programare.
Metoda grafică pentru descrierea algoritmului presupune că pentru descrierea structurii algoritmului utilizat set de imagini grafice (blocuri) conectabile de control al liniei de transmisie. O astfel de imagine este numit de diagrame bloc.
Diagrama de flux - o reprezentare grafică a progresului de rezolvare a problemei. Diagrama bloc este format din blocuri conectate prin linii, iar blocurile sunt afișate sub formă de forme geometrice, numite simboluri. În interiorul un caracter scris instrucțiuni cu privire la funcțiile îndeplinite de bloc - formulă, textul, expresii logice. Tipul de caracter și a alerga norme standardizate scheme logice - GOST 19.701-90 conține o listă de simboluri, numele lor afișate funcții, forme și dimensiuni, precum și punerea în aplicare a regulilor schemei. La elaborarea algoritmului de fiecare acțiune reprezintă bloc corespunzător prezentând secvența lor de linii cu săgeți la un capăt. Elementele de denumiri, identificare și numire flowcharts prezentat în Fig. 1.1.
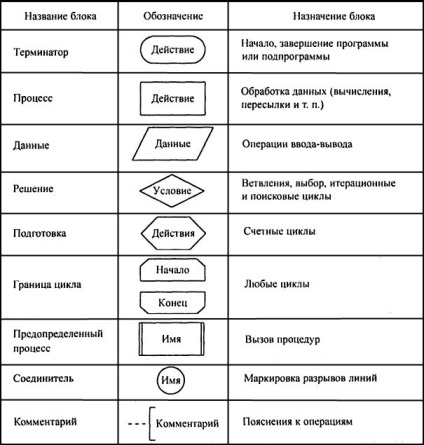
Figura 1.1 - Blocuri de bază
Este demn de menționat câteva reguli de bază de executare organigrame care trebuie urmată în descrierea grafică a algoritmilor. Start algoritmi este marcat cu „Terminator“, din care linia unul. Este scris cuvântul pe butonul „Start“ ( „Acasă“). Algoritmul final marcat cu același simbol, în care cuvântul scris „Stop“ ( „End“). În acest caz, caracterul nu este o singură linie de ieșire, și se poate bloca una sau mai multe linii. „Procesul“ poate avea una sau mai multe linii de intrare și o singură ieșire. În interiorul simbolului de mai multe rețete pot fi înregistrate - în acest caz, acestea sunt executate în ordinea înregistrării. Prezentarea operațiunilor individuale, mai degrabă în mod liber. Pentru a se referă la calcul, puteți utiliza expresii matematice pentru transferul de date - săgeți, alte acțiuni - explică în limbaj natural, de exemplu, A = X + 4; i: = i + 1 -> B.
Pentru a scrie algoritmul de orice complexitate doar trei structuri de bază.
urmați - reprezintă aplicarea consecventă a acțiunii (a se vedea figura 1.2 a.);
ramificare - corespunde alegerii unuia dintre cele două direcții de acțiune (Figura 1.2 b).
ciclu până - definește repetarea acțiunilor, până când condiția este încălcată, a căror îndeplinire este verificată la începutul ciclului (Figura 1.2.).
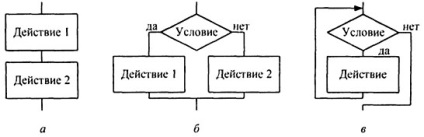
Figura 1.2 - Structuri algoritmice de bază
Mai mult, structurile algoritmice suplimentare sunt utilizate în descrierea algoritmilor. derivați de la bază, din care fiecare poate fi realizată prin intermediul structurii de bază:
selecție - selectarea uneia dintre mai multe opțiuni, în funcție de valoarea unei cantități; (Fig 1.3, și b.)
-Ciclu - repetarea anumitor acțiuni pentru a îndeplini condiția verificării predeterminate care se efectuează după etapele din ciclul; (figura 1.3, d.)
un inel având un anumit număr de iterații (contor buclă) - repetarea anumitor acțiuni specificate de mai multe ori (a se vedea figura 1.3, d, e.).
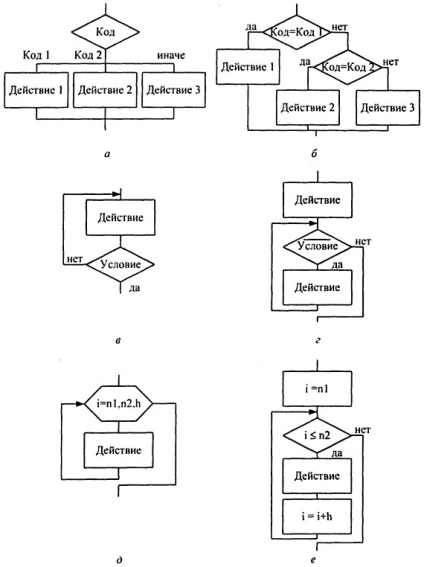
Figura 1.3 - Implementarea structurilor algoritmice suplimentare
peste structura de bază
Luați în considerare exemplele descrierile grafice ale diferitelor tipuri de algoritmi: liniară, ramificată, ciclică și combinate (Figura 1.4 - 1.7.).
Exemplul 1.2. Algoritmul liniar.
Un algoritm de calcul al valorii expresiei K = 3b + 6a (fig. 1.4).
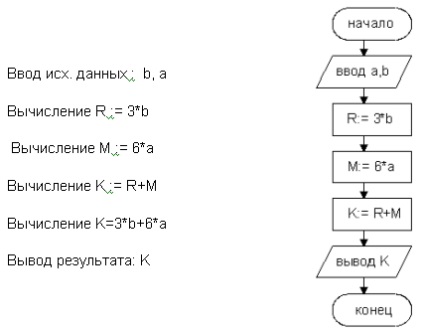
Figura 1.4 - Exemplu Algoritmul organigrame liniar
Exemplul 1.3. Ramificare algoritm.
Algoritmul determină dacă programul trece funcția y = 3x + 4 prin punctul cu coordonatele x1, y1 (fig. 1.5).
Figura 1.5 - Exemplu flowchart ramificare algoritm
Exemplul 1.4. round robin.
Algoritmul determină factorialul unui număr n natural (Figura 1.6.):
Figura 1.6 - Exemplu flowcharts round robin
Exemplul 1.5. Algoritmul combinat.
Este necesar să se determine cel mai mare divizor comun a două numere întregi A și B.
Pentru a rezolva această problemă folosind algoritmul euclidian, care este de înlocuire mai consistentă a numerelor de pe diferența dintre mari și mai mici, până când numerele devin egale. Să luăm în considerare algoritmul pentru cele două exemple.
Exemplu (a): A = 225, B = 125. Aplicarea algoritmului euclidian, obținem pentru A și B, cel mai mare divizor comun al 25.
Exemplu (b): A = 13, B = 4. În acest caz, cel mai mare divizor comun al A și B este egal cu 1.
Algoritmul euclidian schema logică pentru a găsi cel mai mare divizor comun a două numere întregi este prezentată în Fig. 1.7.
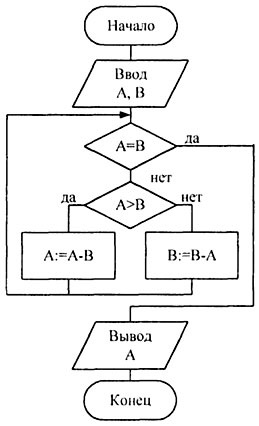
Figura 1.7 - Exemplu flowcharts algoritm combinat
Schema tehnologică prezintă în detaliu toate caracteristicile algoritmului, dar, uneori, un astfel de nivel ridicat de detaliu nu permite identificarea esența algoritmului. În aceste cazuri, descrierea algoritmului folosind pseudocod. Pseudo-cod se bazează pe aceleași structuri de bază ca diagramele bloc ale algoritmului (vezi Tabelul 1.1.).
Algoritmul lui Euclid Exemplul 1.6.Opisanie în pseudocod.
Tabelul 1.1 - Exemplu pseudocod pentru înregistrarea structurilor algoritmice de bază
1.3. Sarcini pentru desen organigrame
Un număr întreg m> 1.
Ia cel mai mic număr întreg k, rezultând în care 4 k> m.
Având în vedere un număr întreg pozitiv n. Calculați produsul.
Având în vedere un număr întreg pozitiv n.
Un n întreg.
Obtineti cel mai mic număr de forma 2 r. n care depășește (r - număr natural).
Având în vedere numerele întregi n, k (n k 0).
Având în vedere un număr întreg pozitiv și n un număr real a.
Având în vedere un număr întreg pozitiv n.
Având în vedere un număr întreg pozitiv n.
Se calculează suma primilor n termeni
Având în vedere o secvență de numere. numărul n - numărul elementelor din secvență și numărul x. Se determină numărul de apariții a unei valori x într-o secvență predeterminată.
Având în vedere un număr întreg pozitiv n. Calculați:
Având în vedere numărul real de un număr natural n.
Având în vedere o secvență de numere și un număr n - numărul de elemente într-o secvență. Găsiți numărul de elemente negative în secvența.
Având în vedere numărul real de un număr natural n.
Să. Găsiți primul membru YN. pentru care inegalitatea. în care - predeterminat număr real pozitiv.
Sunt numere reale a și h, un număr natural n.
Având în vedere un număr întreg pozitiv n. Calculați:
Având în vedere o secvență de numere și un număr n - numărul de elemente într-o secvență. Găsiți suma elementelor pozitive ale secvenței.
Sunt naturale n, x validă.
Având în vedere o secvență de numere și un număr n - numărul de elemente într-o secvență. Găsiți produsul a elementelor negative ale secvenței.
Având în vedere un număr x reală și un întreg n.
Se calculează, fără a utiliza funcționarea exponentiere.
Având în vedere un număr x reală și un întreg n.
Calculați. fără a utiliza funcționarea exponentiere.
Având în vedere un număr întreg pozitiv n.
Sunt numere reale x și, un număr natural n.
Să presupunem că secvența de numere formate prin următoarea lege: = 1; ak = k * ak-1 + 1 / k; k = 1,2. Un n întreg. Ia-o.
Având în vedere un număr întreg pozitiv n. Găsiți numărul de cifre ale numărului și valorii.
Să n număr întreg. Calculați suma.
Având în vedere un număr x reală.
Sunt numere întregi pozitive n, m. Obține suma m ultimelor cifre ale numărului n.
Să n număr întreg. Calculați suma.
Având în vedere un număr întreg pozitiv n.
Dă definiția algoritmului.
Lista proprietățile de bază ale algoritmilor și să extindă esența lor.
Ca clasificate în funcție de tipul de algoritmi implementat printr-un proces de calcul?
Care sunt modalitățile de a descrie algoritmii de știi?
Ceea ce se înțelege prin grafic de a descrie algoritmii? Care este avantajul acestei metode pe descrierea verbală a algoritmului?
Care sunt structurile algoritmice de bază și să explice scopul acestora.
Care este scopul structurilor algoritmice suplimentare? Cum acestea se referă la structurile algoritmice de bază?