Formulele de reducere nu trebuie să-i învețe să înțeleagă. Înțelegerea algoritmul de ieșire a acestora. Este foarte ușor!
Ia cercul unitate și plasat toate măsurile grade (0 °, 90 °, 180 °, 270 °, 360 °) pe acesta.
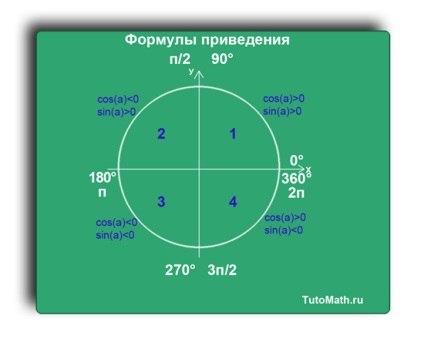
Să analizăm în fiecare trimestru al păcatului funcții (a) și cos (a).
Nu uitați că păcatul funcție (a) se uită la axa Y și cos funcție (a) pe axa X.
In primul trimestru, se poate observa că păcatul funcție (a)> 0. pentru că axa Y este pozitiv în acest trimestru.
Și cos funcție (a)> 0. deoarece axa X este pozitiv în acest trimestru.
Primul trimestru poate fi descris prin măsura gradusnuju ca (90-α) sau (360 + α).
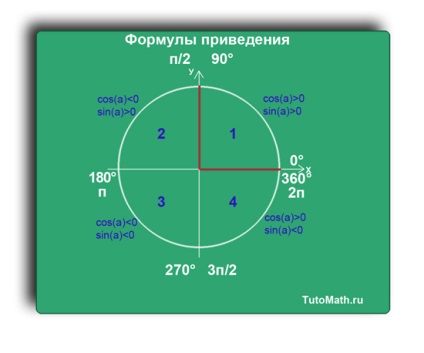
În al doilea trimestru că păcatul funcție (a)> 0. pentru că axa Y este pozitiv în acest trimestru.
A cos funcție (a) 0. deoarece pozitiv axa X în acest cadran.
Al patrulea sfert grad poate fi descris prin măsura ca (270 + α) sau (360-α).
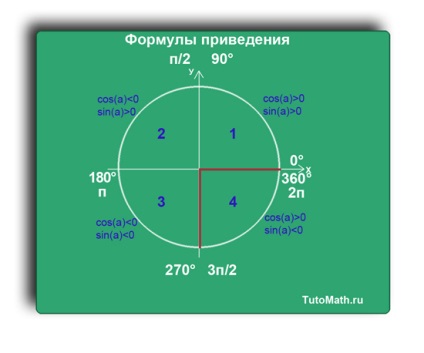
Acum, se ia în considerare formulele de reducere.
Amintiți-vă un algoritm simplu:
1. Cartier. (Se referă întotdeauna la un sfert dintre voi).
2. Conectați-vă. (Pentru trimestrul uite funcția pozitivă sau negativă a cosinusul sau sinus).
3. Dacă în paranteze (90 ° sau π / 2) și (270 ° sau 3π / 2), modificările funcționale.
Și așa va începe să demontați sferturi din acest algoritm.
Afla ce va fi egal cu cos de expresie (90-α)
Vom trece prin algoritmul:
1. Un sfert din prima.
2. În primul trimestru al semnului funcției cosinus este pozitiv.
3. In paranteze este (90 ° sau π / 2), funcția variază în funcție de cosinus și sinus.
Will cos (90-a) = sin (α)
Afla ce va fi egal cu păcatul expresiei (90-α)
Vom trece prin algoritmul:
1. Un sfert din prima.
2. În primul trimestru al semnului funcției sinus este pozitiv.
3. In paranteze este (90 ° sau π / 2), funcția variază cu sinusul și cosinusul.
Va fi păcat (90-α) = cos (α)
Află care este egal cu cos de expresie (360 + α)
Vom trece prin algoritmul:
1. Un sfert din prima.
2. În primul trimestru al semnului funcției cosinus este pozitiv.
3. Parantezele au (90 ° sau π / 2) și (270 ° sau 3π / 2), funcția nu este schimbat.
Will cos (360 + α) = cos (α)
Află care este egală cu păcatul expresie (360 + α)
Vom trece prin algoritmul:
1. Un sfert din prima.
2. În primul trimestru al semnului funcției sinus este pozitiv.
3. Parantezele au (90 ° sau π / 2) și (270 ° sau 3π / 2), funcția nu este schimbat.
Păcătuim (360 + α) = sin (α)
Află care este egal cu cos de expresie (90 + α)
Vom trece prin algoritmul:
1. Un sfert de secundă.
2. În al doilea trimestru al semnului funcției cosinus este negativ.
3. In paranteze este (90 ° sau π / 2), funcția variază în funcție de cosinus și sinus.
Will cos (90 + α) = -sin (α)
Află care este egală cu păcatul expresie (90 + α)
Vom trece prin algoritmul:
1. Un sfert de secundă.
2. În al doilea trimestru al semnului funcției sinus este pozitiv.
3. In paranteze este (90 ° sau π / 2), funcția variază cu sinusul și cosinusul.
Va fi păcat (90 + α) = cos (α)
Află care este egal cu cos de expresie (180-a)
Vom trece prin algoritmul:
1. Un sfert de secundă.
2. În al doilea trimestru al semnului funcției cosinus este negativ.
3. Parantezele au (90 ° sau π / 2) și (270 ° sau 3π / 2), funcția nu este schimbat.
Will cos (180-a) = cos (a)
Află care este egală cu păcatul expresiei (180-α)
Vom trece prin algoritmul:
1. Un sfert de secundă.
2. În al doilea trimestru al semnului funcției sinus este pozitiv.
3. Parantezele au (90 ° sau π / 2) și (270 ° sau 3π / 2), funcția nu este schimbat.
Păcătuim (180-α) = sin (α)
Cearta despre al treilea și al patrulea trimestru al acestui mod de a face un tabel: