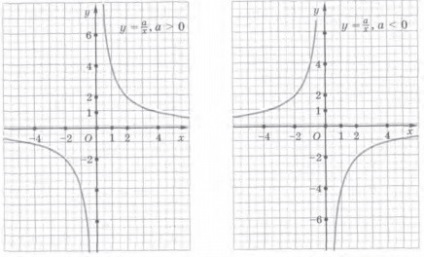
Funcția definită de formula y = a / x. unde x - argumentul, și - un anumit număr de non-zero se numește proporționalitatea inversă. Domeniul acestei funcții - mulțimea tuturor numerelor reale, cu excepția numărului 0. De fapt, dacă valoarea x satisface condiția x ≠ 0, expresia a / x este setat.
Menționăm că, întrucât numărul 0 nu este în domeniul functiei y = a / x. Programul de altfel nu aparține punctului cu abscisa egală cu zero, adică. e. graficul intersectează axa y. Deoarece pentru orice valoare a argumentului x, valoarea lui y nu este zero este, graficul nu se intersectează cu axa x.
Dacă valoarea argumentului x este pozitiv, atunci valoarea lui y este de asemenea pozitiv, în același timp cu creșterea valorilor pozitive ale argumentului x valoarea lui y este redusă și poate deveni mai mică decât oricare număr preselectat mici. Acest lucru înseamnă că, cu o creștere a valorilor pozitive ale punctului argument x de pe graficul funcției se apropie de axa x, dar nu a fost niciodată trecut.
Apropierea pozitivă abscisa zero, face ca valoarea funcției mai mare și mai mare. Aceasta înseamnă că o scădere a valorii punctului de argument x de pe graficul funcției se apropie de axa y. dar niciodată nu a fost trecut.
se comportă în mod similar diagramă și valori negative atunci când argumentul. Când valoarea argumentului x este negativ, atunci valoarea lui y este de asemenea negativ, în timp ce cu creșterea valori negative ale modulului ale valorii unitare argument x y scade și poate deveni mai mică decât oricare număr preselectat mici. Acest lucru înseamnă că, cu o creștere a modulului valorilor negative ale punctului argument x de pe graficul funcției se apropie de axa x. dar niciodată nu a fost trecut.
Apropierea negativă abscisă valorile zero ale modulului de funcții face o mai mare și mai mare. Acest lucru înseamnă că o scădere a valorilor modulului punctului argument x de pe graficul funcției se apropie de axa y. dar niciodată nu a fost trecut.
Graficul de proporționalitate inversă se numește hiperbolă. Spre deosebire de grafica directă proporționalitate, hiperbolă este format din două părți, numite ramuri ale hiperbola.
În general, în cazul în care un> 0, ramurile hiperbola sunt în primul și al treilea trimestru. În cazul în care un <0, то ветви гиперболы находятся во второй и четвертой координатных четвертях.