formula de bază
pendul fizic numit corp solid, care poate pivota în jurul unei axe fixe. Luați în considerare oscilații mici ale unui pendul. poziția corpului, în orice moment dat poate fi caracterizată prin unghiul de deviere de la poziția de echilibru (fig. 2.1).
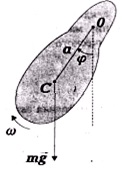
Ecuația momentelor OZ față de axa de rotație (axa OZ trece prin punctul de suspensie O perpendicular planul figurii „pe noi“), neglijând cuplul de frecare, momentul de inerție dacă este cunoscut
Aici - momentul de inerție al pendulului în raport cu axa OZ,
- viteza unghiulară de rotație a pendulului,
Mz = - - momentul de greutate în raport cu axa OZ,
a - distanța de la centrul C de greutate pe axa de pivotare.
Dacă se presupune că, în timpul rotației, de exemplu, unghiul de ceasornic este mărit, punctul de greutate determină o reducere a acestui unghi, și, prin urmare, la momentul Mz<0. Это и отражает знак минус в правой части (1)
Având în vedere că și, ținând cont de fluctuațiile mici, rescriem ecuația (1), sub forma:
(Am luat în considerare faptul că oscilațiile mici. În cazul în care unghiul este exprimat în radiani). Ecuația (2) descrie frecvența de oscilație armonică și perioada ciclică
Un caz particular este pendul fizic pendulul matematic. Întreaga masă a pendulului matematic este practic concentrată într-un singur punct - centrul de inerție al pendulului C. Un exemplu al unui pendul simplu poate servi ca o minge mică solid suspendat pe un fir non-stretch track lung. În cazul unui pendul matematic = l, unde l - lungimea firului, și formula (3) devine cunoscuta formula
Formulele Comparand (3) și (4), se trage concluzia că o perioadă de oscilație al pendulului fizic egală cu perioada oscilațiilor pendul matematic cu o lungime l, numit redus lungimea pendulului fizic:
Perioada de oscilație al pendulului fizic (și, în consecință, lungimea redusă a acestuia) depinde monoton de distanta. Este ușor de văzut dacă, în conformitate cu Huygens-Steiner momentul de inerție teorema exprimată în termeni de moment de inerție în jurul unei axe orizontale paralele care trece prin centrul de masă: Apoi, perioada de oscilație va fi egală cu:
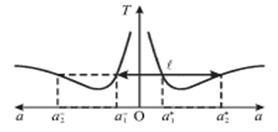
Schimbarea perioadei de oscilație prin îndepărtarea axei de rotație O a centrului de masă în ambele direcții, la o distanță prezentată în Fig. 2.2.
Cinematice oscilații cu pendul
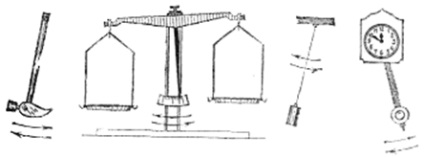
Pendulul este orice organism suspendat, astfel încât centrul de greutate este sub punctul de suspensie. Hammer agățat pe un cui, scalele, greutatea pe coarda - (. Figura 2.3) toate sistemele oscilatorii, cum ar fi un ceas pendul pe perete.
În orice sistem capabil de a efectua oscilații libere, există o poziție de echilibru stabil. Într-un pendul - este o poziție în care centrul de greutate este pe verticală la punctul de suspensie. Dacă ne derivă din această poziție pendul sau împingeți-l, acesta va începe să oscileze, sprijinindu-se într-o direcție sau în cealaltă parte a poziției de echilibru. Cea mai mare valoare din poziția de echilibru până la care pendulul, amplitudinea de oscilație se numește. Amplitudinea este determinată de deformarea inițială sau forța de tracțiune a pendulului a fost pus în mișcare. Această proprietate - amplitudinea condițiilor de la începutul mișcării - nu este unic pentru oscilațiile libere ale unui pendul, dar, de asemenea, în general, pentru oscilații libere ale multor sisteme vibratoare.
În cazul în care este atașat la un pendul apropiat apel - o bucată de sârmă subțire sau un fir de nailon elastic - și va continua să se deplaseze sub ea o placă de sticlă de păr afumat, așa cum se arată în Fig. 2.3. Dacă placa de diapozitive la o viteză constantă pe o direcție perpendiculară pe planul de oscilație, părul de pe placa brăzdat linie ondulată (Fig. 2.4). Avem experiența unui osciloscop simplu - așa-numitele instrumente de vibrații de înregistrare. Curbele sunt înregistrate sub formă de undă de osciloscop sunt numite. Astfel, Fig. 2.2.3. Reprezintă o formă de undă a oscilațiilor pendulului. Amplitudinea de oscilație a acestei forme de undă este reprezentată pe segmentul AB, care dă cea mai mare abaterea unei curbe ondulate dintr-o linie dreaptă ab, că părul să fie trasate pe placa cu pendul staționar (în stare de repaus într-o poziție de echilibru). Perioada reprezentat de segmentul CD, egală cu distanța placa se deplasează pe durata unui pendul.
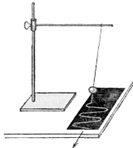
Înregistrarea oscilații pendulului la sooty placa
oscilații oscilogram ale unui pendul: AB - amplitudine, CD - perioada de
Așa cum am muta placa sooty uniform, atunci fiecare mișcare este proporțională cu timpul în care a avut loc. Prin urmare, putem spune că de-a lungul liniei de ab la scară (în funcție de viteza de deplasare a plăcii) arată timpul. Pe de altă parte, într-o direcție perpendiculară ab, un fir de păr pe înregistrare marchează sfârșitul distanței pendulului din poziția sa de echilibru, adică drumul parcurs de capătul pendulului din această poziție. Astfel, forma de undă nu este faptul că, altele decât calendarul - grafic al căii din timp în timp.
După cum știm, panta liniei de pe acest grafic arată viteza de deplasare. După pendulului echilibru poziție se extinde cu cea mai mare viteză. Prin urmare, panta liniilor ondulate din Fig. 2.2.3. cea mai mare la acele puncte în care intersectează linia ab. Pe de altă parte, în momentul deviației maxime a vitezei pendulului egală cu zero. Prin urmare, linia ondulată din Fig. 4 în acele puncte în care este cea mai îndepărtată de ab, are o tangentă paralelă cu ab, m. E. Panta zero.