- f (x)
- la toate punctele în care densitatea continuă p-TION nr. egalitate
Să ne explicăm semnificația titlurilor. „Densitatea de probabilitate-ti“
pe m. în repaus mediu integral. în drepturi. porție este. în cazul în care un punct de Int. .
Să ne imaginăm că int. . bannere. la un punct. moment în care funcția f (x) este continuă. Apoi va căuta la numărul f (), și obținem:
Atitudine, expresie sub semnul limită, există un fel de „credință să fie pe-Tsu-lungime U interval“. Limita acestei relații, ia în considerare atât densitatea de probabilitate în cele mai t .. În fiecare T .. unde f (x) Cont. numărul de f (x) PPSR. cu înțelegerea th densitate ver-ti in t .. QED.
75. exponențial.
Aleatoare X variabilă luând numai valori ne-negative, distribuite exponențial, în cazul în care pentru unii parametri # 955> 0 funcția de densitate este:
f (x) = # 955; e - # 955; x. x≥0
Graficul funcției de densitate
Funcția de distribuție se măsoară prin formula
Substituind expresia funcției de densitate, obținem
F (x) = S x 0 # 955; e - # 955; t dt = -e - # 955; 0 1 t = 1- e - # 955; x. x≥0
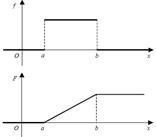
76. Cum este legea de distribuție uniformă pe intervalul [a, b]? Introduceți formula pentru funcția de densitate f (x), găsiți funcția de distribuție corespunzătoare F (x), și complot funcția f (x) F (x).
Noi spunem că variabila aleatoare X. concentrat pe intervalul [a, b], uniform distribuite în acel interval de timp, în cazul în care funcția de densitate este constantă:
Constantă c se determină din condiția:
Legătura dintre funcția de distribuție și densitatea de probabilitate este dată forma prin formula
Substituind funcția f (t), obținem:
77. Este posibilă o distribuție uniformă pe toată axa reală? Care este probabilitatea P (c NE continuă X are o lege uniformă de distribuție în axa întreagă reală, în cazul în care densitatea de probabilitate f (x) este constantă pe axa întregii reale, adică, f (x) = const. 78. Cum este distribuția normală pe linia? Se specifică formula pentru funcția de densitate f (x). obține funcția de distribuție corespunzătoare F (x), și furnizează o formulă de calcul probabilitatea P (# 945; ≤ X ≤ # 946; ). Noi spunem că un continuu variabila aleatoare X respectă o lege de distribuție normală în cazul în care are densitatea de probabilitate de următoarea formă specială: A, și - constante și A> 0> 0. Funcția standard de densitate de înregistrare a legii de distribuție normală. Funcția de distribuție a unei variabile aleatoare normale. Substituind z. Obținem. unde este funcția Laplace. Astfel, funcția de distribuție este o variabilă aleatoare normală: 79. Înregistrarea distribuției densității de variabile x aleatoare normale, pentru care M (x) = m, D (x) = # 948; 2. Cum se schimbă programul distribuției densității, în cazul în care: a) creșterea m, b) crește # 948;? a) că funcțiile grafice f (x) și f (x-a) au aceeași formă deplasând graficului f (x) în direcția pozitivă axei x pe o scară de unități pentru o<0 получим график f(x-a). Отсюда следует, что изменение величины параметра m (математического ожидания) не изменяет формы нормальной кривой, а приводит лишь к её сдвигу вдоль оси Ох. При увеличении m график плотности сдвинется вправо.

2) studiază funcția la extremum.
Când x = m funcție are un maxim
Odată cu creșterea # 948; maxima ordonata curba normala scade, iar curba devine mai plată în sine, și anume comprimată la axa x.
Cum se calculează speranța în cazul distribuției cu densitate f (x)? Poate pentru orice variabilă aleatoare absolut continuă în speranța nu există? Justificați răspunsul.
Așteptarea este absolut continuă NE X cu funcție de densitate f (x) este definit prin: M (X) = xf integral (x) dx de la minus la plus inf inf
Mat. E aleatoare variabilă este valoarea așteptată. În cazul în care limita specificată în partea dreaptă nu există, atunci mat. așteptarea variabilei x este, de asemenea, considerată a fi inexistentă.
În cazul în care X este o variabilă aleatoare discretă ia un set numărabilă de valori posibile, fie. în care mat. există așteptări în cazul în care seria în partea dreaptă converge absolut. pentru că serie se poate abate, acc. variabilă aleatoare și nu poate avea mat. așteptări. În practică, de regulă, o multitudine de valori posibile ale variabilei aleatoare este distribuit doar pe o porțiune limitată axa orizontală, și, prin urmare saltea. există așteptări.
81. Cum se calculează variația în cazul distribuției cu densitate f (x)? Dovedește că variabila aleatoare X cu densitatea de dispersie D (X) nu există, și există speranța matematică M (X).