O scurtă descriere a documentului:
Text Lecții de decodare:
Începem cunoștință cu conceptul de mișcare în spațiu.
În curs de planimetrie sunteți deja familiarizați cu conceptul de mișcare - este o hartă a planului, care păstrează distanța dintre puncte.
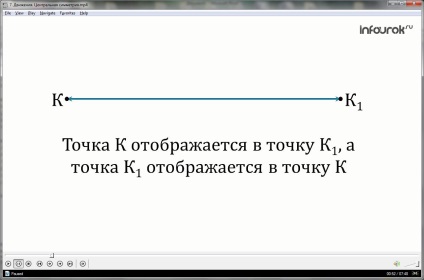
Se spune că o cartografiere a spațiului pe sine, în cazul în care fiecare punct al spațiului alocat la un anumit punct K1, cu orice punct al spațiului K1 a fost stabilit în conformitate cu orice punct K.
Noi spunem că, cu o astfel de afișare punctul K este prezentat (se deplasează) la punctul K1.
Rețineți că un rol special în mapările joc geometria pe sine, păstrând distanța dintre punctele. Ele sunt numite mișcări de spațiu.
Astfel, în cazul în care un punct în spațiu și mișcarea și B se deplasează (afișată) la punctele A1 și B1, apoi AB = a1b1.
Un exemplu este simetria centrală mișcare - este o cartografiere a pe sine, prin care orice punct K la punctul K1 simetric aceasta, în raport cu punctul B. centru de simetrie
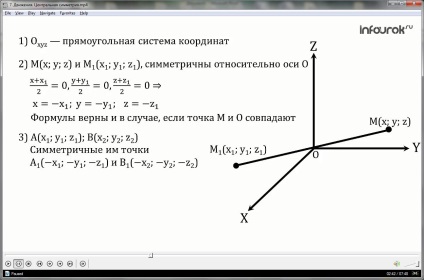
1. Să litera despre centrul de simetrie și de a introduce o cartezian (dreptunghiular) Oxyz sistem cu originea de coordonate în punctul O.
relație 2.Locate între punctele M (x; y; z) și M1 (x1, y1, z1), care sunt simetrice în jurul punctului O.
Dacă M nu coincide cu un centru de simetrie O, atunci G este punctul de mijloc al formulelor coordonate MM1.Togda punctul de mijloc găsim:
x + x1 = 0; y + y1 = 0; z + z1 = 0
Aceste formule sunt valabile și în cazul în care M și G sunt aceleași (explicați-te).
3.Rassmotrim oricare două puncte: A - cu coordonatele (x1, y1, z1) și B - coordonatele (x2; y2, z2), și demonstrează că distanța dintre punctele A1 și B1, că ele sunt simetrice, egale cu AB.
Prin cele de mai sus, avem că punctele A1 și B1 au coordonatele A1 (-X1; -Y1; -z1) și B1 (-x2; -Y2; -z2).
Conform formulei distanțelor între două puncte, vom găsi:
Este clar că AB = a1b1, adică distanța dintre punctele memorate.
Astfel, am demonstrat că simetria centrală a unei mișcări.
Vom aplica aceste cunoștințe pentru a rezolva probleme.
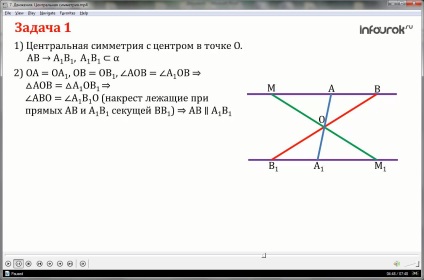
Dovedește că centrul de simetrie al unei linii drepte care nu trece prin centrul de simetrie, este afișat pe o linie paralelă cu aceasta.
1. Luați în considerare simetria centrală cu centrul la punctul O și o linie arbitrară AB, nu trece prin acest punct.
AB direct și punctul O este determinat singur plan α. Punctele A și B sunt afișate în centrul de simetrie în punctul A1 și B1, care se află, de asemenea, în planul a. Și asta înseamnă că întreaga linie A1 B1 se află în planul a.
2. Să se arate că linia AB și a1b1 paralel.
Deoarece simetria centrală, apoi OA1 = OA, OB = unghiul OB1 egal cu unghiul AOB A1OV1 - ca pe verticală, atunci triunghiul este un triunghi AOB A1OV1 primele triunghiuri semn de egalitate.
Din egalitatea triunghiurilor, rezultă că unghiul este egal cu unghiul DLA de a1b1, adică sunt situate transversal perpendicular la intersecția liniilor AB și a1b1 intersectând BB1, prin urmare, liniile drepte AB și a1b1 paralel.
3. Acum arată că este afișat pe a1b1 linie cu simetrie centrală cu centrul la linia O AB. Pentru aceasta este necesar să se demonstreze că un punct arbitrar M al liniei AB se mută la un punct M1 și linia a1b1 punct arbitrar contrar pe linia a1b1 un anumit punct linie simetrică AB.
Luați pe linia AB și orice punct M, diferit de A, și trage linia MO. Această linie traversează a1b1 linie la un moment dat M1.

Simetria centrale, atunci AB = oA1; Unghiul MOA egal cu unghiul M1OA1 ca vertical; unghi MAO egal cu unghiul M1A1 ca culcat în cruce cu linii paralele AB și a1b1 și BB1 secant. Deci, triunghiuri MAO și M1A1 sunt a doua baza egalității de triunghiuri. Din egalitatea triunghiurilor, rezultă că segmentele apărării și OM1 egale, ceea ce înseamnă că punctul M se deplasează la punctul M1. A1b1 situată pe linia de simetrie în raport cu punctul O.
În mod similar dovedit a conversa orice punct M1 linie simetric a1b1 anumit punct M al liniei AB în ceea ce privește punctul O.
Deci, la centrul de simetrie cu privire la o linie care nu trece prin punctul O, acesta este afișat pe o linie paralelă.
Astăzi, am arătat că maparea pe sine, care păstrează distanța dintre puncte, este o mișcare, și, de asemenea asigurat că segmentul de mișcare devine egală cu lungimea de ea, drept - într-o linie dreaptă, un plan - în plan. Un exemplu în acest sens este simetria centrală.