gauss

Două sisteme de ecuații liniare sunt numite echivalente. dacă mulțimea tuturor dintre ele aceleași soluții.

transformări elementare ale unui sistem de ecuații - este:

1. Deleția sistem trivială de ecuații, și anume cele în care toți coeficienții sunt zero;
2. Multiplicarea oricărei ecuații cu un alt număr decât zero;
3. Plus față de orice ecuație orice j -Asta ecuație i-lea înmulțit cu orice număr.

xi Variabila se numește liberă. în cazul în care această variabilă nu este permisă, și întregul sistem de ecuații - este permisă.

Teorema. transformări elementare convertite în sistem echivalent de ecuații.

Sensul metodei Gauss este de a transforma sistemul inițial de ecuații și pentru a obține autorizația echivalentă sau echivalentul a sistemelor incompatibile.

Deci, metoda Gauss constă în următoarele etape:

1. Luați în considerare prima ecuație. Alegeți primul coeficient diferit de zero și să împartă întreaga ecuație pentru ea. Obținem o ecuație în care o variabilă xi este inclus cu coeficient 1;
2. Scăzând această ecuație de restul, înmulțirea cu astfel de numere care coeficienții unei xi variabile rămase ecuații resetare. Un sistem este permisă în xi variabila. și echivalentă cu originalul;
3. Dacă există ecuație banal (rar, dar este, de exemplu, 0 = 0) și ștergeți-le din sistem. Ca urmare a ecuațiilor devine una mai mică;
4. Repetați pașii anteriori până la n ori, unde n - numărul de ecuații din sistem. De fiecare dată când vom alege pentru „prelucrarea“ noua variabilă. Dacă există ecuații contradictorii (de exemplu, 0 = 8), sistemul este incompatibil.

Ca urmare, după câțiva pași obținem orice sistem de autorizare (eventual cu variabile libere), sau incompatibile. Permise de sistem se încadrează în două cazuri:

1. Numărul de variabile este egal cu numărul de ecuații. Prin urmare, sistemul este definit;
2. Numărul variabilelor depășește numărul de ecuații. Punerea toate variabilele libere pe dreapta - obține o formulă pentru variabilele permise. Aceste formule și scrise înapoi.

Asta este! Sistemul de ecuații liniare este rezolvată! Acesta este un algoritm destul de simplu, iar dezvoltarea sa nu se va aplica in mod necesar tutorele matematici superioare. Luați în considerare acest exemplu:

Sarcină. Rezolva sistemul de ecuații:

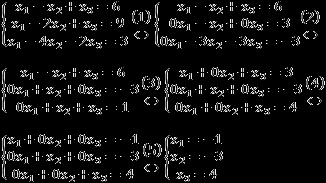
1. Scăzând prima ecuație din al doilea și al treilea - permițând variabila x 1;
2. Inmultiti a doua ecuație cu (-1) și se împarte la a treia ecuația (3) - obținem două ecuații în care o variabilă x 2 include un factor 1;
3. Adăugăm a doua ecuație la prima și a treia - scade. Obținerea autorizației de variabilă x 2;
4. În final, se scade a treia ecuație din prima - pentru a obține permise de variabila x 3;
5. Obținem sistem de permisiune, notați răspunsul.

Soluția generală a unui sistem de ecuații liniare - este un sistem nou, care este echivalent cu originalul, în care toate variabilele sunt exprimate în termeni de liber permise.

Când aveți nevoie de o soluție generală? Dacă trebuie să facă mai puțini pași decât k (k - este cât de multe ecuații). Cu toate acestea, motivele pentru care procesul se termină la un pas l

1. După pasul l -lea dovedit sistem, care nu conține ecuația cu numărul (l + 1). De fapt, este bine, pentru că Sistemul de autorizare va primi în continuare - chiar și pentru câțiva pași înainte.
2. După l-lea pas pentru a obține o ecuație în care toți coeficienții variabilelor egale cu zero, iar coeficientul constant este nenul. Această ecuație contradictorii, și, prin urmare, sistemul este incompatibil.

Este important să se înțeleagă că apariția ecuației contradictorii prin metoda Gauss - este un motiv rezonabil pentru incompatibilitate. În același timp, observăm că, ca rezultat al l-lea pas nu poate rămâne ecuații triviale - acestea sunt șterse în mod direct în acest proces.

Sarcină. Exploreaza compatibilitatea și pentru a găsi o soluție generală a sistemului:

1. Scăzând prima ecuație înmulțită cu 4, de la al doilea. De asemenea, adăugați prima ecuație la a treia - permițând variabila x 1;
2. Scădem treia ecuație înmulțită cu 2, din al doilea - contradictoriu obține ecuația 0 = -5.

Deci, sistemul este incompatibil, deoarece a găsit o ecuație contradictorie.

Sarcină. Exploreaza compatibilitatea și pentru a găsi o soluție generală a sistemului:

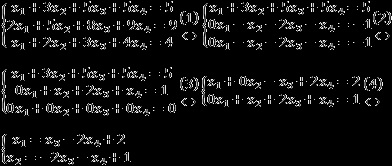
1. Scăzând prima ecuație din a doua (pre-multiplicând cu două) și al treilea - permițând variabila x 1;
2. Scăzând a doua ecuație de a treia. Deoarece toți coeficienții din aceste ecuații sunt aceleași, a treia ecuație va deveni un banal. În același timp, a doua ecuație se înmulțește cu (-1);
3. Scădeți a doua din prima ecuație - obține permisiunea de variabilă x 2. este acum, de asemenea, permisă Întregul sistem de ecuații;
4. Deoarece variabilele x 3 și x 4 - disponibilitatea, transferați-le dreptul de a exprima variabile permise. Acesta este răspunsul.

Astfel, sistemul comun și nesigur, deoarece există două variabile permise (x 1 și x 2) și cele două libere (x 3 și x 4).

1. Lucrul cu formule în problema B12
2. Adunare și scădere a fracțiunilor
3. Teorema lui Vieta
4. Schema generală de soluție de sarcini B15
5. Cea mai mare și cea mai mică valoare

• Pregătirea gratuită pentru examenul de 7 lecții simple, dar foarte util + teme pentru acasă
• 

articole similare

• Metoda Gauss - Mathmetod

• Metoda de introducere a unui parametru, algebra

• RMN - puncte tari, puncte slabe, metode moderne