Prenumerando chirie - o chirie, în care au loc plăți la începutul perioadelor. Prin urmare, fiecare membru al chiriei de rulare pentru o perioadă mai lungă decât chiria postnumerando.
1. Pentru perioada anuitate este de un an, care este, pentru fiecare plată dobânda acumulată timp de un an mai mult. Dacă notăm

,.
2. Pentru



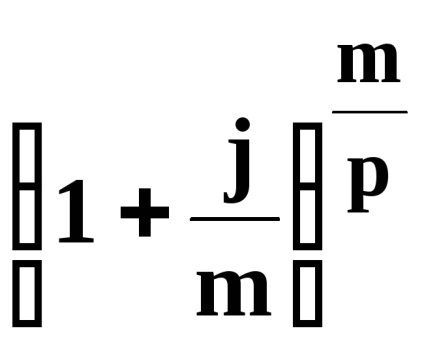
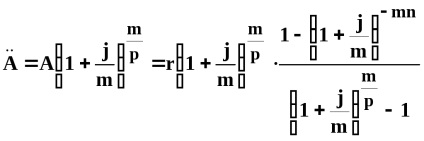

Exemplul 30. Pentru a crea un fond în valoare de 100.000 de ruble la începutul fiecărui an, vor contribui la banca, care acumulează dobânda la depozitele de rată anuală complex de 20% în termen de 5 ani. Găsiți valoarea unei plăți unice.
Decizie. anuităților constituie prenumerando cu parametri.
anuități variabile
Acest tip include chiria financiară, ale cărui elemente sunt modificate în conformitate cu orice regulă. Luați în considerare două tipuri de postnumerando anuitate variabilă.
1. Chiriile cu o creștere absolută constantă


În această secvență anuităților formează o progresie aritmetică, și

.
Înmulțim ambele părți de

.
Scădeți din egalitatea rezultată anterior
.
.
2. Anuitățile cu o creștere relativă constantă


la începutul termenului, vom găsi valoarea actuală
.
Partea dreaptă reprezintă o sumă de progresie geometrică din primul membru
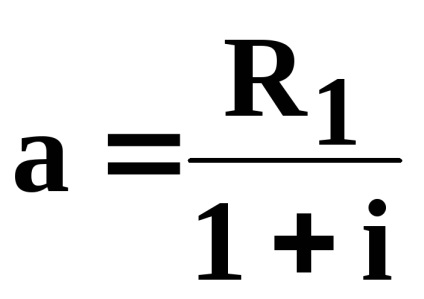
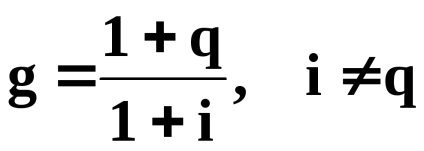
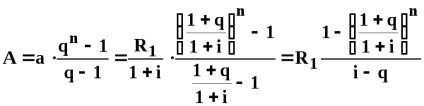
Exemplul 31. Societatea achiziționează o clădire în următoarele condiții: plata timp de 12 ani. valoarea primei plăți anuale (postnumerando)

Decizie. Se inchiriaza cu o creștere absolută

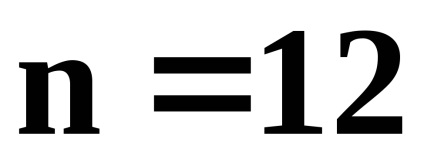
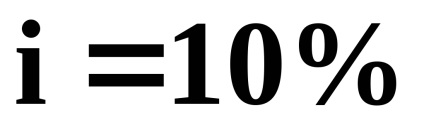
.
Valoarea totală a contractului este rambleu suma tuturor plăților
Notă. la

.
O sumă de rambleu.
Conversia chiriilor financiare
În practică, există cazuri când este necesar să se schimbe condițiile de plată a chiriei, iar aceste condiții nu ar trebui să modifice consecințele financiare ale părților. Luați în considerare diferite cazuri de conversie (de exemplu, schimbarea) chiriile.
1. Rambursarea chiriei. Această înlocuire a one-off plata chiriei. Să fie închiriat cu parametrii specificați. Ea vrea să înlocuiască chiria de plată unică. Definiți dimensiunea plății. Căutând Suma de răscumpărare este egală cu valoarea actualizată a anuităților rambursabile. Desigur, cea utilizată în calcularea valorii actuale a ratei ar trebui să satisfacă ambele părți.
Exemplul 32. Ar trebui să cumpăr pentru 5500 de ruble. de securitate, generând un venit anual de 1.000 de ruble. timp de 7 ani (postnumerando) atunci când se compară rata este de 8%.
Decizie. Venitul este o anuitate cu parametri. Valoarea sa actuală
freca. care este mai mică de 5500 de ruble. Prin urmare, nu cumpara de hârtie.
2. Plata în rate. Aceasta este înlocuirea anuitate de plată unică. Să presupunem că avem obligația de a plăti o anumită sumă. Părțile au convenit că datoria va fi rambursat în forma de plată a chiriei permanente. Părțile prevăd sau suma unei plăți unice sau perioada de plată (presupunând că sunt specificate toți ceilalți parametri). Este necesar să se determine parametrul lipsă. Pentru aceasta echivalează valoarea actuală a chiriei la valoarea datoriei și ecuația rezultată este echivalentă cu determinarea parametrului lipsă.
Exemplul 33. Datoria de 300,000 $. Frecați. Acesta a decis să înlocuiască chiria timp de 5 luni, cu rambursare a datoriei în rate egale, la sfârșitul fiecărei luni. Valoarea datoriei supuse rată a dobânzii de 5% pe lună. Găsiți suma de plată o singură dată.
Decizie. Perioada de inchiriere este de 1 lună. formula anuitate valabilă, în cazul în care.
Sau, folosind coeficientul de reducere anuitate
3. Consolidarea chiriilor. Este o uniune a mai multor chirii unul. Să fie




Din această ecuație găsim parametrul lipsă. Fuzionarea chiria poate fi orice, astfel încât să se calculeze

Exemplul 34. Există două obligații datorii la bancă. Primele plăți semi-anuale în valoare de 100 de ruble. timp de 4 ani. plăți anuale al doilea în valoare de 150 de ruble. în termen de 5 ani. Sa decis să le înlocuiască cu un singur angajament: rate trimestriale egale, timp de 8 ani. Toate plățile sunt efectuate în conformitate cu schema postnumerando. Se determină dimensiunea de plăți unice pentru obligația de înlocuire dacă utilizați o rată anuală complicată de 10%.
Decizie. Prima anuitatea cu parametrii.
Valoarea sa actuală
.
În al doilea rând anuitate anuală cu parametrii.
Valoarea sa actuală
.
Înlocuirea chiria parametrilor.
Valoarea sa actuală
.
Din egalitatea costurilor moderne am primit.
4. Înlocuiți chiria cu unele condiții privind chiria cu alte condiții. Să fie închiriat cu parametrii specificați. Doriți să înlocuiască chiria celorlalți, toți parametrii care, cu excepția unuia, sunt determinate. Trebuie să găsim parametrul lipsă. Este de condiția ca valoarea actuală a ambelor anuități.
Exemplul 35. Părțile au fost de acord să revizuiască termenii împrumutului. Plățile anuale în valoare de 1.000 de ruble. plătit la sfârșitul anului. Înlocuit trimestrial, cu durata totală a creditului rămâne aceeași. Găsiți mărimea plăților trimestriale o singură dată în cazul în care rata dobânzii la împrumut de 15% pe an.
Decizie. Prima anuitatea anuală cu parametri.
Valoarea sa actuală
.
Închiriați de la parametrii a doua.
Valoarea sa actuală
.
Egalăm valoare modernă
Notă. Toate cele de mai sus se aplică tuturor fluxurilor de plată. În orice caz, baza pentru înlocuirea este egalitatea valorii actualizate corespunzătoare a fluxurilor de numerar.
Exemplul 36. Împrumutatul va plăti creditorului 100 de mii. Frecați. după 3 ani și 200 de mii. freca. 4 ani mai târziu. El vrea să restituie le tranșe anuale egale postnumerando timp de 5 ani. Găsiți valoarea plății anuale în cazul în care rata dobânzii la împrumut de 20% pe an.
.
Înlocuirea este chiria anuală pentru o perioadă de 5 ani. Valoarea sa actuală
.
Asimilarea valoare modernă obținem pentru.