Să presupunem că știm traiectoria unui punct material. Acest lucru înseamnă că noi știm dependența r (t). Pentru simplificare, ia în considerare cazul în care traiectoria de circulație se află în același plan (Figura 3.1). În acest caz, un sistem de coordonate carteziene pot fi alese astfel încât una dintre coordonatele, de exemplu z, nu ar schimba, va lua la zero, traiectoria în acest caz, se va afla în planul xOy.
La momentul t1 vectorul raza r egal punct (t1), la momentul t2 - r (t2). In timpul Dt = t2-t1 modificări vector raza de Dr = r (t2) -r (t1). Această schimbare a vectorului raza punctului material determină vectorul său de deplasare în timpul t.
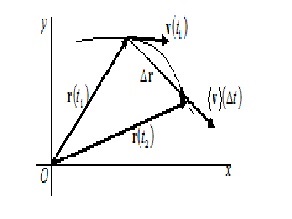
Noi definim viteza medie a corpului pe intervalul de timp Dt urmează:
Dacă un punct material se mișcă uniform într-o linie dreaptă, viteza medie astfel determinată descrie pe deplin toate caracteristicile unei astfel de mișcări.
Într-un caz arbitrar, este clar că vectorul v este în nici un fel de legătură cu calea de deplasare a corpului. Se trece la limita, putem determina viteza de deplasare a corpului la un anumit interval de timp (în acest caz, în momentul t1):
Astfel, am determinat vectorul vitezei corpului la un anumit moment, ca derivat al vectorului razei în raport cu timpul a corpului. Sunt trei denumiri ale derivatului utilizat în literatura de specialitate. Se observă că vectorul viteză astfel determinat este asociat în mod unic cu traiectoria de deplasare a corpului - este îndreptată la o tangentă la aceasta. Vectorul vitezei de mișcare a corpului poate schimba ca modulul și direcția.
Într-un sistem de coordonate cartezian:
Dr vector definește deplasarea vectorului a corpului în intervalul de timp Dt, calea parcursă de către organism în acest timp s. Acesta va fi determinat de lungimea curbei - Lot traiectoriei. Numai cu mișcare rectilinie modul vector de deplasare este egal cu calea corp traversat, cu condiția că direcția vectorului nu se schimbă viteza. Dacă luăm o foarte mică parte a unei traiectorii arbitrare, acesta va fi o linie dreaptă, pe care corpul se mișcă uniform într-o linie dreaptă.
Modulul vectorului de viteză se poate scrie:
,
din moment ce. Ceea ce arată că drumul parcurs de corp, este determinată numai de vectorul vitezei și timpul unitatea de mișcare:
Lăsați amploarea schimbărilor de viteză cu timpul după cum se arată în figura 2.2.
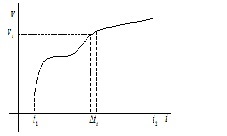
Pentru a determina calea parcursă de organism în timpul unui interval de timp finit Dt se împarte în N intervale D t i:
.
Calea traversat în timpul acestor intervale de timp:
.
cale completă traversat de corp, va fi egală cu suma:
.
În același timp, aproximativ, calea către zona i-lea poate fi definită ca:, atunci distanța parcursă este aproximativ egală cu:
.
Valoarea exactă a distanței parcurse obține trecerea la limita:
Limita corespunzătoare se numește definit integrala.
Am identificat viteza unui corp într-un anumit cadru de referință. Ne găsim relația dintre vectorii vitezei corpului în (punctului material) definit în două cadre diferite K și K „(figura 2.3). La un moment dat, în poziția de timp a corpului în aceste sisteme este determinată de r și r vectori raza de referință“. Se vede că r = r0 + r“. Dacă sistemul K“și corpul în mișcare, apoi, după o diferențiere timp obținem:
În cazul în care partea superioară a K „sistem pentru a plasa al doilea corp, atunci (2.5) ne permite să determinăm viteza corpului în raport cu a doua (viteza relativă): v“ = v-v0.
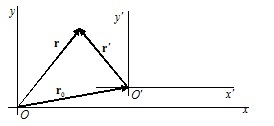
Vectorul de viteză al punctului material în sistemul K este egal cu vectorul de viteză în K „sistem plus viteza K vector“ sistem definit în K sistem de coordonate.
In concluzie, definim viteza medie a corpului (valoarea medie a vectorului de viteză a modulului) în intervalul de timp Dt. Este egal cu traseul parcurs de organismul împărțit de către toate mișcarea:
În mod similar, această definiție viteza medie, putem defini valoarea medie a oricărei cantități fizice care depinde de timp:
În special, folosind definiția generală (2.7) pentru a găsi valoarea medie a vectorului de viteză, obținem expresia (2.1).