Redactare. Sunt numere reale a. b și c. și amenda de 0. Rezolva pătratic ecuația ax 2 + bx + c = 0 sau raportează că nu există soluții reale.
Decizie. De la algebră știm că:
uravnenieax pătrat 2 + bx + c = 0, vyrazhenieD = b 2 - 4 ac - discriminant:
- esliD> 0 are două soluții. ;
- esliD = 0 are o soluție unică;
- esliD <0, не имеет действительных решений.
Prin urmare, avem nevoie pentru a calcula discriminante (notoriu pentru variabila lui d reală de tip real) și, în funcție de valoarea sa de a organiza o sucursală. În primul rând, trebuie să verificați dacă ecuația are soluții reale (pentru a face capul variabilelor x 1 și x 2 tipuri de reale). Dacă este așa, și dacă discriminante nu este egal cu zero, vom calcula ambele soluții conform formulelor, iar daca discriminantul este zero, atunci vom calcula o soluție unică. În cazul în care nu există soluții reale, obținem un mesaj text despre el. Algoritmul de bază este ilustrată prin următoarea diagramă de flux:
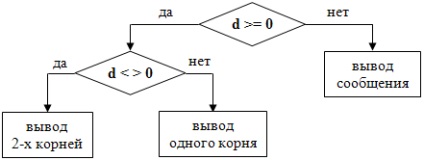
Trei bloc nedescifrate sunt declarații de ieșire standard. Să le examinăm în detaliu.
1) În derivarea celor două rădăcini ale expresiei va fi după cum urmează:
x1: = (-b + sqrt (d)) / 2 * a;
x2: = (-b - sqrt (d)) / 2 * a;
writeln ( 'x1 =', x1: 4: 2, 'x2 =' x2: 4: 2);
În acest caz, expresia afișată ar arata astfel: „x = 1 m. x 2 = n“. care este evidențiat în albastru constante de text fără echivoc, care sunt luate din lista de argumente pentru writeln. Valorile calculate x 1 și x 2. Mai mult decât atât, rădăcinile sunt obținute într-o formă formatat primul număr după colon specifică o lățime câmp pentru variabila de ieșire cu o perioadă (când deficitul domeniu va extinde programul), iar numărul de după colon doilea - - roșu numărul de caractere afișat fracționată (nu poate fi modificată în timpul funcționării programului);
2) În derivarea aceeași rădăcină - este afișată toate la fel, doar o singură rădăcină:
3) În absența rădăcinilor reale ale mesajului:
writeln ( 'Nu există soluții reale!');
Ca rezultat, interior inclusive corp condițională va arăta astfel:
în cazul în care d <> 0 apoi începe
x1: = (-b + sqrt (d)) / 2 * a;
x2: = (-b - sqrt (d)) / 2 * a;
writeln ( 'x1 =', x1: 4: 2, 'x2 =' x2: 4: 2)