
flacon de sticlă Klein
Ocazional găsit sub forma unui pahar de suveniruri sticle de Klein. Pentru fabricarea de astfel de sticle au nevoie de sticlar de înaltă calificare. La punctul în care sticla se intersectează, din motive tehnologice trebuie să lase o gaura.
De „Futurama“ serialul TV în seria «traseul All Evil» bere pe raft arată Klein, care este imbuteliat in sticla Klein.
În carte, Aleksandra Miticha „Jocul de giveaway“ eroi ajunge în spațiu, cum ar fi o sticlă Klein
poezie umoristică Victor Lebedev
Două matematică în grădină
Sărbătorirea o zi de naștere.
Unul a adus alimente cu ei,
O alta - sticla Klein.
Unul a întrebat: „Cum să bea vin
În cazul în care sticla este bidimensională?
Dupa ce de echitatie aici este numit în partea de jos,
Și există perete, poate? "
O alta a spus: „Nu te teme,
Și bea-ka ohotku!
Mobius mi-a spus că
Vin vodca mai puternic. "
Am ascultat prietenul nostru săraci,
Pentru buze feluri de mâncare lui.
În cazul în care el a dispărut brusc și altele asemenea,
Nu voi spune.
Klein sticla cu mâinile
Magazin sticle de sticlă Klein
Jocuri Torus joc gratuit software-ul pentru Windows și Mac OS X, care arată topologia și sticla Torul Klein
suprafaţă Klein
Klein sticla, suprafață unilaterală închis (vezi fig. Suprafețele fe), introduse în considerare de către Klein (1874). C. n. Se poate obține din tubul (fig .. A), deschis pe ambele părți, în cazul în care, tub îndoit, trece un capăt mai îngustă ea prin perete și „lipici“ (identificat) ambele cerc de delimitare, curbare exterior, o gamă largă de interior și un interior, cerc mai îngust spre exterior. Astfel. se obține suprafața (Fig .. b) care are o linie de auto-intersecții. K. n. Fără a auto-intersecție poate fi realizată numai în spațiul patru-dimensional.

Fig. art. suprafata Klein.
Marii Enciclopedii Sovietice. - M. sovietic Enciclopedia. 1969-1978.
ecuația Gordon - Klein
Kleynmihel Petr Andreevici
. Uită-te la alte dicționare:
Suprafață Klein - Klein sticla cufundat în spațiu tridimensional. Klein sticla este o anumită suprafață non-orientabile (manifold adică bidimensional). Klein sticla a fost descrisă pentru prima dată în 1882 de matematicianul german F. Klein. Aceasta este strâns legată ... Wikipedia
suprafata Klein - sticla Klepna închis cu o suprafață unilaterală a genului I (a se vedea figura 1, a, b ..). C. n. Se poate obține din ABCD pătrat (vezi. Fig. 2) identificarea punctelor de segmente AB și CD, situată pe liniile drepte paralele cu latura AD, iar punctele din segmentul BC și AD, ... ... Enciclopedia de matematică
Surface - Acest termen, există alte utilizări, a se vedea de suprafață (valori) .. Un exemplu de un simplu nume tradițional Suprafețe pentru mnogoie bidimensional ... Wikipedia
Klein - NISHYNY FORMULA - expresie pentru differents. foton scattering secțiune transversală ds de un electron (a se vedea. efectul Compton). Laboratorul. Sistemul de coordonate unde frecvența incidentului și fotonii împrăștiate, unghiul solid pentru foton imprastiere parametrul împrăștiată unghi r0 = e2 / mc2 = ... ... fizic Encyclopedia
Surface - (Surface, Oberflache). Fiecare liniyumozhno continuă curba prezent ca o urmă a unui punct în mișcare. ca acest lucru și orice formă P.mozhno sau descrie mișcarea în spațiu a unui tip sau variabilă invariabilă krivoylinii și mărimea ... Enciclopedia de Brockhaus și Efron
Suprafața Klein - sticla Klein cufundat în spațiu tridimensional. Klein sticla este o anumită suprafață non-orientabile (manifold adică bidimensional). Klein sticla a fost descrisă pentru prima dată în 1882 de matematicianul german F. Klein. Aceasta este strâns legată ... Wikipedia
Suprafața (geometrie) - Exemplu Suprafețe simple de nume tradiționale pentru colectorul bidimensional în spațiu. Suprafața este definită ca un set de puncte ale căror coordonate satisfac un anumit tip de ecuație: Dacă ... Wikipedia
suprafață - f. suprafață, față, zona de suprafață; interfata, interfata, suprafață de delimitare; regresie de suprafață, suprafața de regresie; suprafata Klein, sticla Klein ... dicționar rusă-engleză a termeni matematici
Surface - (Surface, Oberfläche). Fiecare linie curbată continuu poate fi reprezentat ca o urmă a unui punct în mișcare. La fel ca acest lucru, și fiecare GP pot fi formate sau pentru a descrie mișcarea în spațiul unei linii curbe de tip sau variabilă și invariabilă ... ... Collegiate dicționar FA Brockhaus și IA Efron
Klein sticla - Klein sticla cufundat în spațiu tridimensional. Klein sticla este o anumită suprafață non-orientabile (manifold adică bidimensional). Klein sticla a fost descrisă pentru prima dată în 1882 ... Wikipedia
Klein sticla - este o anumită suprafață non-orientabile (manifold adică bidimensional ..). Klein sticla a fost descrisă pentru prima dată în 1882 de matematicianul german F. Klein. Aceasta este strâns legată de banda Möbius și planul proiectivă. Numele aparent provine dintr-o traducere greșită a cuvântului german Fläche (de suprafață), care este în limba germană este aproape în ortografia cuvântului Flasche (sticla).
Pentru a construi un model de sticla Klein, trebuie să ia o sticlă cu două deschideri: în partea de jos a și în perete, trage gât, îndoiți-l în jos și vinde-l printr-o gaură în perete sticla (pentru sticla Klein reală în spațiu cu patru dimensiuni de gaura nu este necesară, dar fără el nu se poate face în spațiu euclidian tridimensional), atașați la orificiul de pe partea de jos a sticlei.
Spre deosebire de sticlă obișnuită a acestui obiect nu are nici o „margine“, în cazul în care suprafața se termină brusc. Spre deosebire de balonul poate trece de la calea către exterior în interiorul fără să traverseze suprafața (m. E. Nu „în interior“ și nu „în afara“ este de fapt acest obiect).
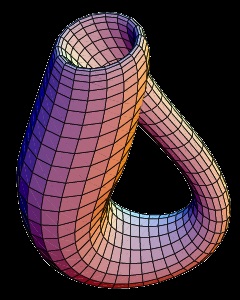
Klein sticla cufundat în spațiu tridimensional.
Ca o bandă Mobius, sticla Klein este o varietate diferențiabilă non-orientabile bidimensională. Spre deosebire de banda Möbius, sticla Klein este un colector închis, atunci există o varietate compactă, fără limită.
Klein sticla nu poate fi încorporat (scufundat numai) în tridimensional spațiu R³ euclidian, dar încorporate în R4.
Klein sticla poate fi obținut prin lipirea a două benzi Mobius pe margine.
Suprafata numar cromatica este 6.