Atunci când se deplasează spre dreapta de la centrul de asimetrie va fi caracterizat printr-un număr pozitiv, atunci când deplasat spre stânga - negativ.
Coeficientul de asimetrie (AA) se calculează ca al treilea ordin raport momentul central al pătrat la cub mediei
ungulate: variații în Whitlock. T3.
După cum vom vedea, coeficientul de asimetrie - un al treilea moment de ordin normalizat (T3). Se crede că curbele cu valoarea absolută a indicelui de asimetrie A *> ± 0,5 considerabil caracterizat
offset. Dacă A ^ ± 0,25 - asimetrie neglijabilă.
Grăitor (Figura 8) descrie asimetrie a curbei fire de direcție mai lung ( „clopot“).
Dacă t = 0 - distribuție simetrică, dacă A1> 0 - distribuția are
asimetrie dreapta; în cazul în care 1 <0 - левосторонняя асимметрия.
Curbele prezentate în Figura 8 ilustrează simetria și permite celor două cele mai comune tipuri de asimetrie de distribuție. În distribuție simetrică (a) media aritmetică, modul și mediana sunt egale. Pentru curbele asimetrice ale acestor valori statistice sunt inegale. Mai mult decât atât, media aritmetică și mediana sunt compensate de la centru spre curba fire lungi. Deoarece media aritmetică (x) de „audiere“ în poziția „bine“ mai îndepărtate de modul (M0) a punctelor de curbă, iar mediana (e) „încet“, media (x) este deplasat mai mult decât mediana (m e). În acest caz, mediana este între

Fig. distribuție 8. Forme pentru diferite valori ale factorului de asimetrie (A *)
modă și media aritmetică.
După cum puteți vedea, direcția de asimetrie este stabilită geometric foarte simplu. Cuantificati gradul de asimetrie impune găsirea de gradul algebrică.
Exemplu. Conform unui număr discret de gospodării de distribuție statistică a randamentului culturilor de cereale nevoie pentru a măsura cantitativ asimetria unei variante de distribuție în eșantion. Pentru a găsi valoarea coeficientului de asimetrie prin formula nevoie pentru a efectua calcule suplimentare de mai sus. Ultimul 38 sunt prezentate în tabelul.
Datele de ieșire și calculate pentru a calcula asimetrici (t) și ekspesu)

= D * .- x) 2 - 2 _ = _ = _ 238.9 39.3 Conform calculelor preliminare, avem: 57.
Deviația ° standard, cantitatea este:
a = l / 7 d / 39,3 = 6,3 ^
Valoarea momentului centrale de ordinul trei ^
X) n = 3 și a = 79,4 523,6 '
Am obținut din expresia 57.
Înlocuind valorile lui q și q 3 în coeficient formulă asimetrie, avem:
O valoare pozitivă a indicelui * indică distribuția asimetria dreptul fermelor în ceea ce privește randamentul și valoarea sa absolută este de 0,25 <| 0,3181 <0,5 | означает наличие умеренной асимметрии в исследуемом ряде распределения.
In concluzie, trebuie remarcat faptul că cantitatea de realizare predominantă într-un număr de distribuție mai mic de asimetria medie a eșantionului este negativ. În cazul în care numărul de variante este dominat de variații în mărime mai mare decât media, va exista o asimetrie pozitivă.
Partea negativă a coeficientului de asimetrie ca măsuri de asimetrie, trebuie să menționăm că această cifră nu are nici o limită superioară sau inferioară. dimensiuni deosebit de mari a coeficientului de asimetrie este, practic, aproape nici un spațiu.
De asemenea, considerată o metodă de evaluare a gradului de asimetrie, există alte tehnici metodologice. Ele fac obiectul unui curs special.
Pentru stabilirea gradului de deviere de la distribuția normală calculează o măsură a aplatizării (E *). Ea caracterizează abaterea de la distribuția normală cu întruchiparea propulsiei sau căderea nodului curbei de distribuție. În cazul în care acționează dispozitivul de blocare vârfuri aplatizare numit pozitiv, atunci când cade - negativ.
Pentru peakedness măsurare cantitativă utilizată momentul centrală a patra comandă (^ 4). Raportul dintre abaterea standard a acestuia din urmă la un al patrulea raport se numește gradul de peakedness (aplatizării). care este
calculat normalizat momentul a patra comandă). În cazul în care baza de comparație pentru a lua o distribuție normală, raportul
De aceea, factorul peakedness sau pur și simplu „aplatizării“ (Ex) va fi exprimată prin formula:
În cazul în care gradul de peakedness Normal, E = 0. Pentru distribuțiile gostrovershinnih exces este pozitiv (E * ^ °), pentru partea superioară plată - negativ (E * = 0). Formularul „Top“ pentru aceste cazuri sunt prezentate în grafic (fig. 9).
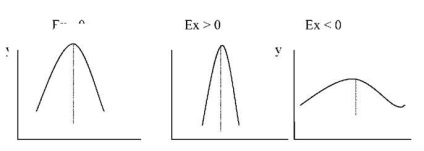
Fig. 9. Distribuția formelor pentru diferite valori în exces (*).
În cazul în care valoarea indicelui de aplatizării * „curba este considerată slaboekstsesivnoyu. Cea mai mare valoare absolută a coeficientul de boltire negativ este minus 2. Când această valoare scade la curba vertex abscisă și curba de distribuție este împărțită în două curbe unimodale distincte.
Trebuie remarcat faptul că termenul „excesul“ de origine greacă (kitishiz), și numele de formă aplatizării în diferite curbe de distribuție sunt rădăcina cuvântului. Aceasta se referă curbele strichkokurtichni, platokurtichni și mezokurtichni (Fig. 10).
Fig. 10. Tipuri de aplatizare: a - strichkokurtichny b - platokurtichny în - mezokurtichny
Conform calendarului, curba strichkokurtichnoi (a) se caracterizează prin plasarea majoritatea unităților de observare în apropierea centrului. În curba platokurtichnoi caz (forma silueta de platou) variantelor îndepărtate semnificativ de centrul de distribuție (b). Moderate plasat în jurul unei forme variante a centrului de distribuție determină aplatizării mezokurtichnoi ca curba (c).
Pentru curba de distribuție normală (x = 0 ° = 1) Valoarea kurtotica (E *) a coeficientului este 0.263. Astfel, valoarea sa este calculată cu formula:

unde ^ 3 + ^ -, respectiv, a treia și prima cuartilă;
U9 °> și 10 - a noua și a zecea percentila yanostiy.
Astfel, coeficientul de kurtosis este raportul dintre jumătate amplitudinea diferenței dintre quartilele 90-lea și 10 percentile lea. (Valorile care caracterizează diviziunea de distribuție în patru, zece și o sută de părți egale sunt numite cuartile, respectiv, decil și percentile).
Conform distribuției companiilor de cereale randament valoarea aplatizării este (Tabelul 38.):
Conform valorilor indicelui de aplatizare calculat (E =
0,52), curba de distribuție se caracterizează prin ușoară ekstsesivnistyu formă platokurtichnoyu, adică forma curbei pe grafic - plat depasit.