[Articolul] Algoritmul
Noi rezolva problema folosind adancime de căutare.
În cazul unui grafic direcționat proizvedom o serie de runde. Adică, fiecare din partea de sus, pe care nu le-am vizitat, veți găsi în profunzime, care este la intrarea summit-ul va fi să-l picteze gri, iar atunci când ieși din ea - în negru. Și, în cazul în care algoritmul încearcă să meargă la partea de sus a gri, aceasta înseamnă că ciclul este găsit.
În cazul unui graf neorientat. o muchie nu trebuie să aibă loc într-un ciclu de două ori prin definiție. Prin urmare, trebuie să fie evaluate că curentul vizualizat de la marginea de sus nu este yavlyaetya marginea prin care am ajuns la acest vârf.
Rețineți că, dacă graficul are vârfuri cu bucle, atunci algoritmul va funcționa corect, ca atunci când începe căutarea în adâncime de la un top, există o margine de lider în ea la fel, ceea ce înseamnă că această buclă va fi un ciclu.
Pentru recuperarea ciclului de deschidere suficient de căutare în profunzime din partea de sus a altul pentru a adăuga acest vârf în stivă. În cazul în care adâncimea-prima căutare a găsit în partea de sus a, care se află pe un ciclu, va elimina în mod constant în partea de sus a stivei nu este încă satisface găsit din nou. Toate nodurile îndepărtate vor sta pe o buclă necunoscută.
Ciclul de căutare Asymptotics coincide cu comportamentul asimptotic în adâncimea de căutare -.
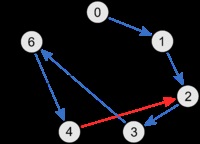
Moment ciclu petrecut: fin albastru - deja finalizat, marginea roșu este în gri, deja un trecut, de top.
[Articolul] Dovada
Având în vedere un grafic. Run. Luați în considerare a efectua procedura de căutare în profunzime a unui nod. Din moment ce toate nodurile gri se află pe recurență stiva, pentru ei vârf este accesibil, între nodurile adiacente din stivă au o margine. Apoi, dacă se consideră că din partea de sus există un avantaj într-un top gri, aceasta înseamnă că, din partea de sus există o cale spre și dinspre partea de sus există un mod în care constă într-o singură muchie. Și, din moment ce ambele aceste căi nu se intersectează, ciclul acolo.
Arătăm că dacă graful conține un ciclu, se va găsi întotdeauna. Să - primul vertex aparținând ciclului, discutat în căutarea adâncime. Apoi, există un vârf aparținând buclei și având o margine în partea de sus. Deoarece de la partea de sus la partea de sus există un drum alb (care se află pe același ciclu), apoi prin Lema despre cai albe în timpul procedurii de căutare în profunzime din partea de sus, partea de sus este gri. Din cauza un avantaj în, atunci această margine într-un top gri. Ca urmare a găsit un ciclu.