Într-o proiecție paralelă a cercului pe orice P * plan obține poza ei, în cazul general, sub forma unei elipse.
Oricare ar fi planul circumferențială a fost localizat, este recomandabil să se construiască un prim paralelogram A * B * C * D * - proiecție paralelă a unui ABCD pătrat, descris despre o anumită circumferință, iar apoi folosind opt opt puncte și tangent pentru a intra în ea elipsă.
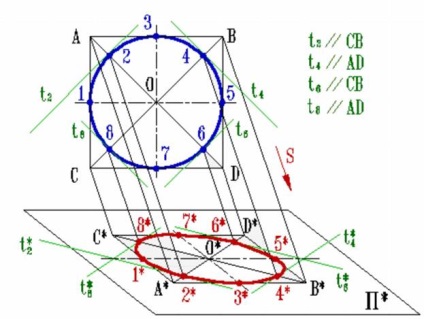
Punctele 1, 3, 5 și 7 - mijlocul laturilor unui paralelogram. Punctele 2, 4, 6 și 8 sunt dispuse pe diagonală, astfel încât fiecare dintre ele se divide poludiagonal la un raport de 3: 7.
Într-adevăr, putem scrie că A2 / 1D = A * * 2/2 * O * bazat pe proprietățile proiecției paralele Dar A1 / 1o = (r√2-r) / r≈3 / 7.
Din cele opt tangenta la elipsa primele patru - această parte a paralelogramului, iar restul t2, t4, t6 și t8- linii paralele cu diagonalele. Deoarece t2 * tangent la elipsa este paralelă cu diagonala C * D *, aceasta se explică prin faptul că t2 * și C * D * sunt proiecțiile celor două linii paralele și CD-ul t2.
reprezentări grafice, înainte de desen al elipsei, este recomandabil să efectuați următorii pași:
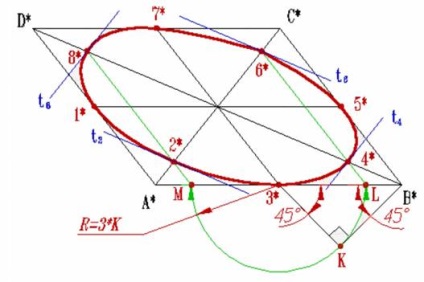
Construiți o vedere în perspectivă a unui pătrat - paralelogramul A * B * C * D * și țineți pe diagonală A * C * și B * D *;
Marcați punctele mediane ale părților laterale ale paralelogramului - punctul 1 *, 3 *, 5 * și 7 *;
In intervalul 3 * B *, ca ipotenuza construct isoscel dreptunghiular triunghi 3 * KB *;
Din punctul 3 * 3 * Raza K descrie un semicerc, care se intersectează cu A * B * la punctele L și M; Aceste puncte împart etapa 3 * A * și este egală cu ea 3 * B * segment în raport de 3: 7;
Prin punctele L și M să dețină laturi drepte paralele paralelogramului și marcați punctul 2 *, 4 *, 6 * și 8 * sunt situate pe diagonalele;
Construiți o tangentă la elipsa în punctele găsite. t2 Tangent și t6 paralel cu BD și t4 și T8 tangenta paralel cu curent alternativ.
După ce a primit opt puncte și aceeași tangenta, cu o precizie suficientă pentru a reprezenta grafic o elipsă.
GOST 2.317-69 definește poziția cercurilor situate în planuri paralele cu planul de proiecție pentru rectangular dreptunghiular izometrice și cu diametre.
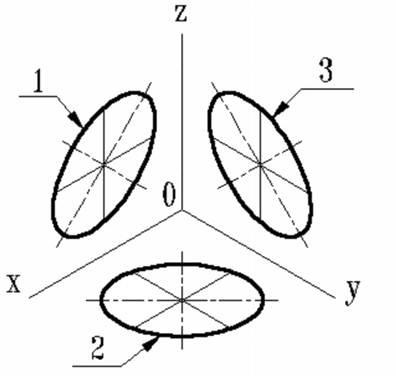
proiecție izometrică a cercurilor,
situate în planuri paralele cu planurile proeminentelor
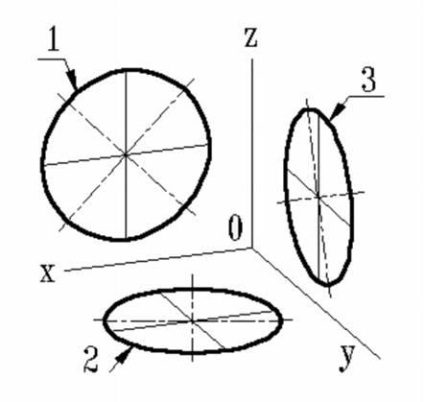
proiecție Dimetric de cercuri,
situate în planuri paralele cu planurile proeminentelor
Dacă proiecția izometrică funcționează fără distorsiuni a axelor x, y, z, axa mare a elipselor 1,2, 3 este 1,22, iar axa mică diametrul cercului -0.71.
Dacă proiecția izometrică funcționează cu distorsiunea axelor x, y, z, axa mare a axei elipse este 1, 2, 3 este egal cu diametrul cercului, și un mic - diametrul 0,58 circumferința.
Dacă dimmetricheskuyu proiecție funcționează fără distorsiune a axele x și axa z ale elipselor mari 1, 2, 3 este egal cu 1,06 diametrul cercului și axa mică a elipsei 1 - 0,95, elipsele 2 și 3 - 0.35 diametrul cercului.
Dacă funcționează dimetric cu distorsiunea proiecția axele x și z, axa mare a elipselor 1, 2, 3 este egal cu diametrul cercului, elipsa și axa minoră din 1 - 0,9, elipsele 2 și 3 - 0,33 diametrul cercului.
1-elipsă (axa mare dispuse la un unghi de 900 față de axa y); 2-elipsă (axa mare dispuse la un unghi de 900 față de direcția axa z); 3-elipsă (axa majoră 900 este înclinată față de axa x).