determinată experimental legea lui Coulomb și principiul superpoziției poate descrie complet câmpul electrostatic al unui sistem dat de taxe într-un vid. Cu toate acestea, proprietățile câmpului electrostatic pot fi exprimate într-o altă, mai formă generală, fără a recurge la noțiunea de domeniul Coulomb unui punct de sarcină.
Prezentăm o nouă cantitate fizică ce caracterizează câmpul electric - vector de câmp electric fluxul φ. În spațiul în care un câmp electric, este un mic suficient loc de joaca dS. Produsul zonei modul vector pe δS și cosinusul unghiului a dintre vectorul și normala la site-ul este numit un vector elementar intensitatea curentului prin δS zonei (Figura 1.3.1.):
unde En - modulul componentă normală de câmp
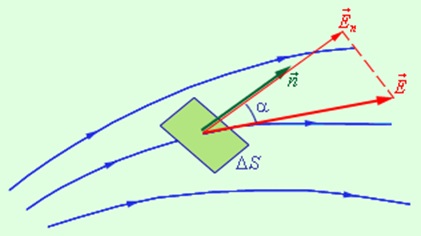
Prin definiție, un δφ flux elementar
Să considerăm acum unele arbitrare suprafață închisă S. Dacă vom rupe suprafața mici din zona δSi. identifica fluxuri elementare câmp δφi prin aceste zone mici, iar apoi acestea sunt însumate, rezultatul obținem φ flux vector prin suprafața S închisă (Figura 1.3.2.):
În cazul unei suprafețe închise este întotdeauna ales normala exterioară.
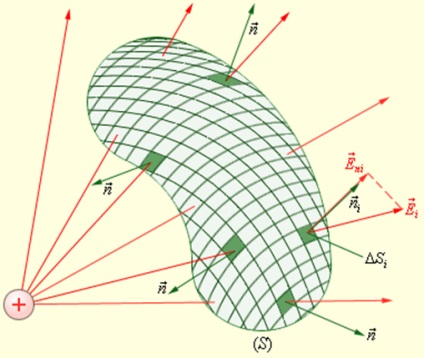
Calcularea fluxului F printr-o suprafață închisă arbitrar S
stări teorema lui Gauss:
Curgerea vectorului intensitate polyacherez electrostatic arbitrară suprafață închisă este egală cu suma algebrică a taxelor, situate în interiorul suprafeței, împărțit la ε0 electric constant.
Pentru a dovedi acest lucru să ne considerăm mai întâi suprafața sferică S. centrată pe sarcină q punct. Câmpul electric în orice punct al sferei perpendicular pe suprafața sa și este egală cu modulo
unde R - raza sferei. Curgerea φ prin suprafața sferică este egală cu aria de produs a unei sfere pe E 4πR 2. Prin urmare,
Acum înconjoară punctul de încărcare suprafață închisă arbitrar S și ia în considerare sprijinirea unei sfere de rază R0 (fig. 1.3.3).
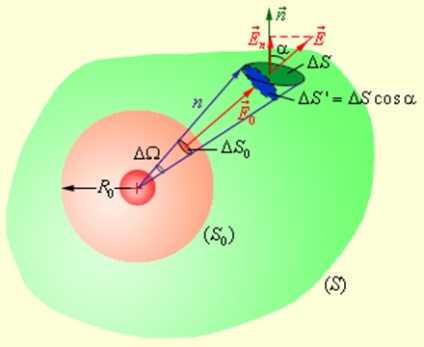
Hraneste punct de taxa de câmp electric prin orice suprafață care înconjoară taxa S.
Să considerăm un con cu un unghi mic solid la δω vertex. Acest con aloca zonă mică sferă δS0. și pe suprafața S - δS zona. fluxuri elementare δφ0 și δφ prin intermediul acestor site-uri sunt aceleași. De fapt,
Acolo δS „= δS cos α - MarketPlace alocate con cu un unghi solid în sfera de rază δω n suprafață.
Din moment. o, Prin urmare, rezultă că fluxul electric printr-o suprafață totală de încărcare punct arbitrar, anexând taxa, egală cu φ0 fluxului prin suprafața zonelor auxiliare:
În mod similar se poate demonstra că, dacă o suprafață S închisă nu include un punct de sarcină q. pârâului φ = 0. Un astfel de caz este reprezentat în Fig. 1.3.2. Toate liniile de câmp electric de încărcare punct pătrunde prin suprafața închisă S. În interiorul suprafeței S a taxelor nu este, astfel încât în acest domeniu linia de alimentare nu se rupe si nu apar.
Generalizarea teoremei Gauss la o distribuție arbitrară a taxelor rezultă din principiul superpoziției. Domeniul de orice distribuție de sarcină poate fi reprezentat ca o suma vectorială a câmpului electric de sarcini punctiforme. taxe de sistem de curgere printr-o suprafață cp arbitrar S închisă va consta din fluxul φi câmpuri electrice de taxe individuale. În cazul în care taxa qi S. suprafața a fost în interiorul acestuia contribuie la egalitatea de flux, dacă această taxă este activată în afara suprafeței, apoi contribuția sa la fluxul câmpului electric este egal cu zero.
Astfel, teorema Gauss.
Teorema lui Gauss este o consecință a legii lui Coulomb și principiul superpoziției. Dar dacă acceptați declarația conținută în această teoremă pentru axioma inițială, atunci ar fi o consecință a legii lui Coulomb. De aceea, teorema lui Gauss este numită uneori formularea alternativă a legii lui Coulomb.
Folosind teorema lui Gauss, este posibil, în unele cazuri, pentru a calcula cu ușurință câmpul electric în jurul unui corp încărcat, având în vedere în cazul în care distribuția de încărcare are o simetrie și structura globală a câmpului poate avansa ghici.
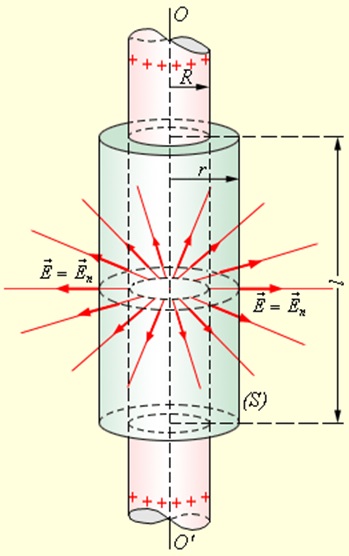
Un exemplu este problema de calcul domeniul pereți subțiri, tubulare încărcat uniform cilindru lung R. rază Acest obiectiv are o simetrie axială. Din motive de simetrie, câmpul electric trebuie să fie orientată radial. Prin urmare, pentru a aplica teorema Gauss este recomandabil să se aleagă o suprafață S închisă sub forma unui cilindru coaxial cu raza r și lungime l. închis la ambele capete (Fig. 1.3.4).