Momentele de inerție I-beam
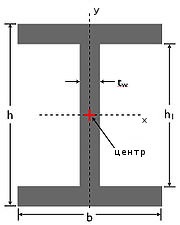
Momentul de inerție pentru a calcula de fază I (a se vedea. Figura)
- b - lățimea rafturilor de-a lungul axei x,
- h - înălțimea unui fascicul I în direcția y
- tw - grosimea peretelui miezului
- H1 - distanța dintre cele două rafturi (înălțime de perete)
Din proprietate, că momentul de inerție a unei figuri complexe este suma momentelor de inerție ale componentelor sale putem obține momentul de inerție I-beam în raport cu axa x:
momentul dreptunghiular de inerție A:
$$ I ^ _ = \ frac $$
Momentul de inerție al dreptunghiului B și C:
$$ I ^ _ ^ _ = I = \ frach_ ^ 3> $$
Apoi, un moment de fază I de inerție la axa x:
Momentul de inerție al I-beam în raport cu axa y
aici:
AB = suprafața unui dreptunghi B (sau C): [matematica] a_b = \ frach_1 [/ math]
x = distanța de la centrul dreptunghiului B (sau C) de grinda axa y I: [matematică] x = \ frac [/ math]
Deoarece axele X și Y sunt axe de simetrie, statice momentele Sx și Sy sunt zero.
Programul de calcul simplu al caracteristicilor geometrice ale unui fascicul I
Momentele de inerție axial ale profilelor laminate
Momentele de inerție axial ale profilelor laminate (I-beam, unghiuri, canale) sunt evacuate din sortimentul de laminate. în conformitate cu numărul de profil.