Schimbul de căldură se efectuează prin transfer de căldură cu transfer de masă la mișcarea lichidă sau gazoasă se numește transfer de căldură prin convecție. Transferul de căldură convectiv două componente se pot distinge: convecția pura. și anume Numai transfer de căldură din cauza transferului de masă și de conductivitate termică. și anume transfer de căldură molecular, care este încă realizată în lichid sau gaz.
transfer de căldură convectiv - este convectiv de transfer de căldură între curentul de fluid sau gaz și contactarea acestuia cu o suprafață solidă. La calcularea căldurii utilizate lui Newton drept Richman:
,
în care tpov - temperatura de suprafață cu care are loc schimbul de căldură, tsr - temperatura de tur. În problemele convectivi coeficientul de transfer termic α este valoarea dorită. Experimental poate fi definită ca densitatea fluxului termic la suprafața de delimitare a mediului, împărțită la diferența dintre temperaturile lor.
Convecție poate fi liber (naturale) sau forțată. convecția naturală apare ca urmare a unei distribuții neomogene de densitate în volumul mediului într-un câmp gravitațional extern. convecția forțată are loc sub acțiunea forțelor externe aplicate la limitele volumului de lichid sau gaz, în detrimentul raportate anterior energiei cinetice (pompă, vânt, ventilator).
2. Proprietățile fizice ale mediului (lichid sau gaz).
Procesul de transfer de căldură convectiv depinde în mod esențial de proprietățile fizice ale mediului în mișcare. Pe lângă deja cunoscută pentru a ne caracteristicile mediului termic
(C, λ, ρ. A). Rolul important jucat de mutarea mediul μ său coeficient de vâscozitate. proprietate Vascozitatea au toate mediul real. Prezentați vâscozitatea după cum urmează. Sa observat că între straturi adiacente de lichid care se deplasează cu viteze diferite, o forță de frecare internă se opune mișcării. Conform legii lui Newton, această forță pe unitatea de suprafață este proporțională cu gradientul vitezei în direcția normală la direcția de deplasare:
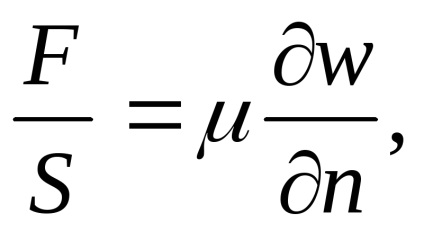
ν = μ / ρ. Este ușor să se determine dimensiunile acestor factori:
║μ ║ = kg / (m * c) = H * s / m2 = Pa * s; ║ν ║ = 2 m / s. Coeficienții de vâscozitate poate depinde de temperatură.
3. Ecuațiile diferențiale ale transferului termic convectiv.
Atunci când se analizează curenții în sisteme deschise, procesul de transfer de căldură este în general considerată izobară. Prin urmare, cantitatea de căldură transportată de către mediul, este de obicei asociată cu transferul de entalpie. În cazul în care mediul de a aloca un plan, ca urmare a convectie in timpul dτ transferat se va încălzi prin acesta Q1-2 = dmh1-2 = ρwdτЅh1-2. Apoi, fluxul de căldură asociat cu convectie, va fi egal cu ρwh1-2. o densitate a fluxului de căldură, în legătură cu o conductivitate termică egală -λgradt. În formă vectorială, fluxul de căldură pentru transferul de căldură convectiv poate fi scrisă ca:
Pentru a determina coeficientul de transfer termic al câmpului de temperatură și de sistem găsirea folosind ecuațiile de transfer convectiv de căldură, care constă din următoarele ecuații:
ecuațiile de mișcare a mediului (într-un sistem de coordonate cartezian, - proiecțiile lor pe x, y, z);
Ecuația de transfer de căldură la limita solidului și lichidului.
3.1. ecuația de continuitate
Această ecuație rezultă din legea conservării masei, care pot fi rezumate după cum urmează:
Viteza Viteza
= Aderarea acumulare - ingrijire
greutate greutate greutate
Pentru a obține expresia matematică a acestei legi, este necesară într-un sistem de coordonate cartezian să aloce un volum elementar al mediului, sub forma unui cub cu margini dx, dy, dz și ia în considerare masa de flux prin fiecare față. Dacă fluxul se deplasează la o viteză w. că, în direcția x peste dydz feței în timpul fluxului dτ mediu în masă. Prin fața opusă a aceleiași zone implică în masă. Diferența dintre acestea este masa în exces (acumulare) în masa preferată per volum elementului scheth - componenta de curgere: Același considerent trebuie să cheltuiască componentele dlyay- si Z- debitului. Apoi, în valoare de ea va fi viteza acumulării de masă în volum elementar dV:
Expresia din acolade reprezintă divergența (ρw). De aceea, în cele din urmă, ecuația de continuitate (sau discontinuitate) este scrisă ca:
În cazul densitate constantă, ecuația (2) este transformată în
Ecuația (3) - o ecuație de continuitate pentru fluide incompresibile.