Cercul este o curbă plană închisă fiecare punct care este echidistant față de un punct dat (centrul cercului). Distanta de la orice punct de pe cercul \ (P \ stânga (\ dreapta) \) la centrul său se numește raza. centrul cercului și cercul se află în același plan. Ecuația cercului de rază \ (R \), cu centrul la origine (ecuația canonică a unui cerc) are forma
\ (+ = \).

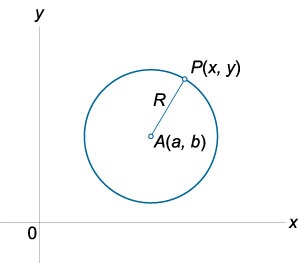
Ecuația unui cerc cu raza \ (R \), cu centrul într-un punct \ arbitrar (A \ stânga (\ dreapta) \) este scrisă ca
\ (\ Dreapta) ^ 2> + \ dreapta) ^ 2> = \).

Ecuația cercului în formă parametrică
\ (\ Stânga \<\begin x &= R \cos t \\ y &= R\sin t \end \right. \;\;0 \le t \le 2\pi\),
unde \ (x \) \ (y \) - coordonatele punctelor circumferință, \ (R \) - raza cercului, \ (t \) - un parametru.
Ecuația generală a unui cerc
\ (A + A + Dx + Ey + F = 0 \)
cu condiția \ (A \ ne 0 \) \ (D ^ 2 + E ^ 2> 4AF \).
Centrul cercului este situat la coordonatele \ (\ la stânga (\ dreapta) \), în cazul în care
\ (A = - \ mare \ frac> \ normalsize, \; \; b = - \ mare \ frac> \ normalsize \.)
raza cercului
\ (R = \ sqrt + - 4AF >>> \ normalsize> \)
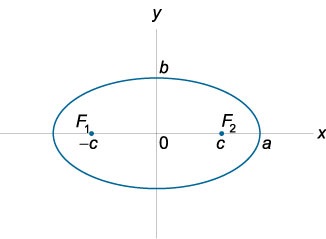
Se numește curba elipsă plat pentru fiecare punct în care suma distanțelor dintre două puncte date (focarele elipsei) este constantă. Distanța dintre focii se numește lungimea focală și este notat cu \ (2c \). Mijlocul segmentului care unește focarele se numește centrul elipsei. Elipsei are două axe de simetrie: prima sau axa focală care trece prin focalizarea și perpendicular pe a doua axă. punctul de intersecție al axelor elipsei sunt numite noduri. Segmentul care leagă centrul elipsei cu vârful numit axele elipsei. Axa semimajore este notat cu \ (a \), axa mică - prin \ (b \). Elipsa al cărui centru se află la originea, iar jumătatea de linia situată pe liniile de coordonate, este descrisă de ecuația canonică.
\ (\ Mare \ frac >>>> \ normalsize + \ mare \ frac >>>> \ normalsize = 1. \)
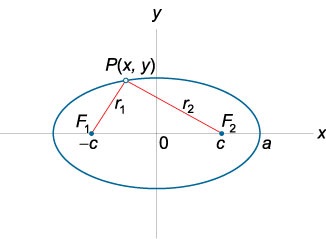
Suma distanțelor din orice punct al elipsei la focarele sale este constantă:
\ (+ = 2a \),
în cazul în care \ (\) \ (\) - (P \ left (\ dreapta) \) distanța de la un punct \ arbitrar la focarele \ (\) și \ (\) \ (a \) - axa semimajore a elipsei.
Raportul dintre semi-axele elipsei și o lungime focala
\ (= + \)
unde \ (a \) - axa semimajore elipsei, \ (b \) - axa mică, \ (c \) - jumătate din lungimea focală.
excentricitatea de elipsă
\ (E = \ mare \ frac \ normalsize 0 \).
Perimetrul elipsei
\ (L = 4AE \ stânga (e \ dreapta) \),
unde \ (a \) - semiaxa mare a elipsei, \ (e \) - excentricitate, \ (E \) - integrală complet eliptic al doilea tip.
Formulele aproximative pentru elipsa perimetrului
\ (L \ approx \ pi \ stânga [\ normalsize \ stânga (\ dreapta) - \ sqrt> \ right] \; \; L \ approx \ pi \ sqrt +> \ dreapta)> \)
unde \ (a \) \ (b \) - axa elipsei.
Zona elipsei
\ (S = \ pi ab \)