Fizica - știința naturii, în sensul cel mai general. Ea studiază diferite fiind substatsii (materie, domeniul substanță) și formele cele mai simple ale mișcării sale, precum și interacțiunea fundamentală. natura, controlează mișcarea materiei.
Mecanica - ramura a fizicii, studiind. mișcarea corpurilor materiale, precum și interacțiunea dintre ele.
Cinematica - o secțiune a mecanicii care studiază descrierea matematică a mișcării corpurilor fără a ține seama de cauzele de mișcare.
Dinamica - secțiunea a mecanicii care studiază cauzele mișcării mecanice.
modele de bază abstracte ale corpurilor reale un punct material - are o mulțime de, dar nu are dimensiunea;
corp rigid - volumul de dimensiuni finite, complet umplut cu substanța, distanța dintre oricare două puncte ale mediului de umplere a volumului nu se schimbă în timpul mișcării
1.1 scalar - valoare fizcheskaya. care este determinată numai de valoarea.
Vector - Valoarea fizcheskaya, care este determinată nu numai de valoare, dar, de asemenea, direcția.
vector Geometric este reprezentat ca un segment de linie direcționat, care este o lungime scara - unitatea vector.
O cantitate vector este notată cu o cantitate fizică corespunzătoare cu o săgeată pe ea: vectorul .Modul notat fără săgeți: | | sau V.
Orice vector poate fi reprezentat ca suma mai multor vectori.
Înlocuirea unui vector cu suma vectorială a mai multor altor numit extinderea vectorului în componente. componente vectoriale, desigur, de asemenea, vectori. Descompunerea vectorului în componente pot produce un număr infinit de moduri, la fel ca orice cantitate scalară poate fi extins într-un număr infinit de moduri de termeni.
Cel mai adesea produc vectori de descompunere în direcțiile axelor unui sistem de coordonate cartezian definit. Prin selectarea unui sistem de coordonate specific, poate fi caracterizat printr-o mărime vectorială și semn al componentelor sale, nu este îndreptat spre direcția lor.
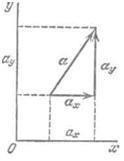
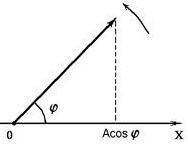
componenta de valoare, luată cu semnul său, numit proiecția vectorului în direcția vectorului respectiv unitatea de axe - un vector. Valoarea absolută a care este unitatea.
Vectorii de unitate sunt adesea asociate cu axele de coordonate ale sistemului de coordonate (în special, cu axele unui sistem de coordonate cartezian). Direcțiile acestor vectori coincid cu direcțiile axelor respective și încep adesea aliniate cu începutul sistemului de coordonate.

1.3 Adăugarea Vectra
plus grafic și scădere. Reguli și triunghi parallleogramma. scăderea vectorilor
Metoda analitică de adunare și scădere

Regula pauză - închidere a adunat poligon.
1.4 Multiplicarea vectorilor

1.4.1 1.4.2 1.4.3 1.4.4 1.4.5
un produs vector al unui produs cruce vector pe vektorovi
vectori de transformare forfecare:
= +. X = ax + x 'y = ay + y' ... în timp ce porniți. x = h'cosa - y'sina, y = x'sina + y „cosa
după inversie. x = -x 'y = -y' ... = pseudovectors axial - coordonatele sunt inversate la inversarea sistemelor de coordonate
vector = true polar - coordonatei nu sunt modificate în timpul inversiunii sisteme de coordonate
dvuhvektorov produs 7.Skalyarnym este un număr egal cu produsul dintre modulii acestor vectori cosinus
Din fizica este cunoscut faptul că activitatea atunci când se deplasează forța F S este A = F S • • cosj m. F. = A (F • S).
Derivata funcției f (x) la x0 este raportul limita increment Δf funcția în acest moment la bH argumentul increment atunci când acesta din urmă tinde la zero (infinitezimal mic). Este scris ca. LimΔx → 0 (Δf (x0) / Ax) = limΔx → 0 ((f (x + Ax) -
derivat. Derivatul la punctul x 0 este egal cu panta tangentei la graficul funcției y = f (x) la acel moment.
produsul vectorial 8.Vektornym pe de
vector este un vector care are următoarele proprietăți: Lungimea sa este egală cu
Vector c este perpendicular pe planul în care se află vectorii a și b
Vector este direcționat în așa fel încât rotirea vektorak vektoruosuschestvlyaetsya invers acelor de ceasornic, dacă
văzute de la sfârșitul vectorului (în acest caz, spunând că triplă vektorovi - dreapta).
Vector produs este egală cu aria paralelogramului construit pe vectorii
produs 9.Smeshannym a trei vectori
, este un număr egal cu produsul vectorial,
înmulțit cu vectorul.
Produsul amestecat este egal cu volumul paralelipipedului construit pe vectorii
Integral - una dintre cele mai importante concepte ale matematicii, care au apărut în legătură cu necesitatea, pe de o parte, pentru a găsi derivați de funcții ale acestora (de exemplu, pentru a găsi o funcție care exprimă traseul parcurs de un punct în mișcare, în acest punct de viteză), iar pe de altă parte - pentru a măsura suprafața, volumul , lungimea arcului, forțele de muncă pentru o anumită perioadă de timp, etc. Integrarea - .. procesul de identificare a integralei.
Funcția Primitive - o funcție, care este un derivat al acestei funcții pe întregul domeniu. Integrala nedefinită a funcției - mulțimea tuturor primitivelor unei funcții date.
integral Definite unei funcții continue este egal cu diferența dintre valorile indefinit integrală cu limitele superioare și inferioare.
Semnificația geometrică a definit integralei. Dacă f (x)> 0 pentru
interval [a, b], suprafața integrală este curbată ABCD trapez.
2.1 Conceptul de derivat și differetsiala funcției scalare a unei variabile.





Trei moduri de sarcini de mișcare.
Poziția punctului în ceea ce privește sistemul otschѐta (O), vector raza zadaѐtsya, de la început provedѐnnym otschѐta înainte de a trece la punctul M.
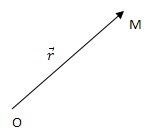
Legea ecuației vectorului de mișcare zadaѐtsya:
În cazul în care poziția de coordonate fel punctul zadaѐtsya oricare trei coordonate.
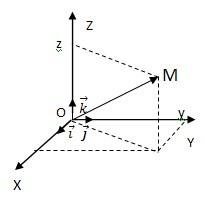
Dacă selectați un sistem cartezian rectangular, legea de mișcare a M zadaѐtsya punctul trei ecuații de coordonate:
se aplică această metodă, în mod normal, dacă se cunoaște punctul traiectorie în raport cu otschѐta sistemului selectat.
Poziția punctului M este determinată de distanța
selectat din traiectoria care începe otschѐta măsurate de-a lungul căii și să ia cu legea aplicabilă. Legea ecuației mișcării zadaѐtsya
.
Traiectoria - o linie continuă, care descrie punctul în mișcare svoѐm. Ecuația traiectoriei poate fi obținută din ecuațiile cinematice ale mișcării, cu excepția unui timp. Ecuația traiectoriei se referă coordonatele punctelor:
.
Mutarea - provedѐnny vector din poziția inițială până la punctul final.
Vectorul de expresie se deplasează prin incrementarea vectorului rază și coordonatele
;