Multe probleme practice sunt reduse la cazul în care trebuie să fie găsiți o valoare maximă sau minimă a funcției f (x1 x2, ..., xn.):
și pe x1 variabile. x2. ..., xn a impus diverse restricții sub formă de inegalități sau egalități:
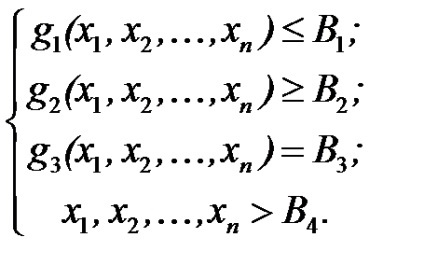
Funcția (1.1) se numește funcția obiectiv (funcția obiectiv, funcție liniară, formă liniară).
(1.2) - (1.5) sunt condițiile de intrare de constrângeri (restricții inegalități, restricții de sistem) funcția (1.1).
Programare - găsirea unui extremum (max sau min) funcția (1.1) cu constrângerile date (1.2) - (1.5), adică cu alte cuvinte, pentru a găsi soluția optimă pentru funcția f (x1. x2. ..., xn) cu restricții impuse.
programare liniară (probleme de programare liniară) - este de a găsi o soluție optimă (planul optim), cu condiția ca funcția obiectiv f (x1 x2 ..., xn ..) este liniar, toate condițiile și restricțiile sunt x1 liniare. x2. ..., xn ≥ 0.
Să presupunem că există n variabile x1. x2. ..., xn. Este necesar de a găsi astfel de valori ale acestor variabile pentru a atinge maxim sau min funcție obiectiv (liniar):
cu sistem de restricție adecvat:
Pentru o anumită problemă practică a sistemului de limitare poate cuprinde oricare dintre semnele de inegalitate. Dar x1 foarte variabilă. x2. ..., xn trebuie să fie întotdeauna mai mare sau egală cu zero.
Este necesar să se găsească o soluție la limitările sistemului X = (x1. X2. ..., xn), în cazul în care funcția obiectiv (1.6) va avea o valoare extremă (max sau min). În acest caz, soluția trebuie să respecte constrângerile de sistem (1.7). Găsirea unei astfel de decizii și a problemei programării liniare (LP).
problemă de programare liniară poate fi scrisă într-o formă mai concisă:
Problema generală de programare liniară este problema în sistem care limite pot fi atât inegalitate și egalitate (sistemul (1.8)).
Problema standard liniară programată Ia este problema, sistemul de restricții care constă doar în unele inegalități și tot necunoscut este mai mare sau egal cu zero:
Canonical problemă de programare liniară este problema, care este de a determina valoarea maximă (minimă) a sistemului de funcții și constrângere obiectiv, care constă numai dintr-una din ecuațiile (toate variabilele necunoscute trebuie să fie mai mare sau egal cu zero)
Liniar problemă de producție ilizadacha privind utilizarea rațională a capacității de producție (resursele disponibile), este una dintre primele sarcini pentru care metoda programării liniare. În general, modelul matematic al problemei poate fi formulată după cum urmează.
Compania produce tipuri de produse, cu grupuri de echipamente. Cunoscut timp standard pentru procesarea fiecărui element în fiecare grup de echipamente (de exemplu, minute sau ore) și timpul de funcționare a fondului de echipamente de fiecare grup. Necesar pentru a face planul de producție în care societatea va avea cea mai mare rentabilitate.
i - numărul grupului de echipament (i = 1,2, ..., m);
j - numărul unui produs (j = 1,2, ..., n);
aij - rata de timp pe unitatea de procesare j- produs in j- th gruppeoborudovaniya th;
bi - fond de timp de funcționare a grupului de echipamente lea j-;
cj - profit pe produs -j mii de specii;
xj - numărul planificat de unități J- produs mii;
- planul de producție dorit.
Indiferent de programul de producție. componentele sale trebuie să îndeplinească condiția: timpul total de prelucrare a tuturor produselor din acest grup de echipament nu trebuie să depășească momentul fondării echipamentului de grup.
unități de procesare X1 a primului produs asupra grupului i -lea hardware pentru a fi cheltuite AI1 unități de timp x1; unități de procesare x2 din al doilea produs din același grup de echipamente vor petrece timp de unități AI2 x2 și t. d.
Timpul necesar pentru procesarea tuturor produselor pe grupul i-lea de echipamente este egal cu suma ().
Această sumă nu poate depăși durata de funcționare a fondului i -lea gruppyoborudovaniya, t. E. Trebuie să fie mai mică sau egală cu. Scrierea unor astfel de condiții pentru toate grupele de m Echipamente formiretsya sistem:
pentru că componente ale planului, de fapt, o serie de produse și, prin urmare, nu pot fi exprimate în numere negative, apoi se adaugă în mod natural condiții
.
În cazul în care planul de producție () venitul de afaceri va fi egal cu
Este necesar să se facă programul de producție, astfel încât funcția F a luat cea mai mare valoare posibilă atunci când toate condițiile.
sistem liniar de inegalitățile (1.11) și forma liniară (1.12) formează un model matematic al problemei utilizării raționale a capacităților de producție. Dintre toate soluțiile sistemului inegalităților liniare (1.11), care satisfac condiția non-negativitate variabilelor, este necesar să se găsească o soluție, în care forma liniară (1.12) ia valoarea maximă posibilă. Aceasta este - problema programării liniare.
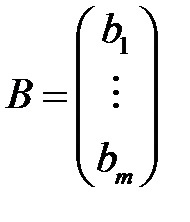
Parametrii inițiali ai problemei poate fi reprezentat ca o matrice Un cost resursă specifică a vectorului de resurse și un profit specific vector C:
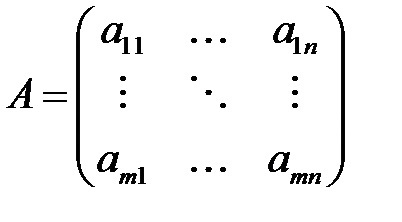
Problema de programare liniară clasică - problema distribuției programului de producție.
Asociația de producție a primit o comandă pentru fabricarea de n tipuri de produse în cantități d1. d2. ..., Dn, respectiv. Unificarea m întreprinderile subordonate, fiecare dintre care poate fi făcută o comandă pentru orice produs.
bi - timpul efectiv de funcționare fond a întreprinderii i-lea;
aij și cij - respectiv rata de timp de aplicare și costul de fabricație al produsului j -lea unitate la m întreprinderii j-;
xij - numărul de produse J- specii th, care i se solicită să pregătească o întreprindere i-lea.
Provocarea este de a găsi distribuirea comenzilor între întreprinderi, care minimizează costul total de producție a tuturor produselor
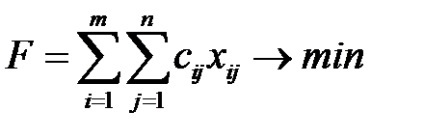
cu condiția ca limitele să fie îndeplinite de timpul de funcționare al fondului fiecărei întreprinderi
și va fi produs un număr necesar de elemente de fiecare tip
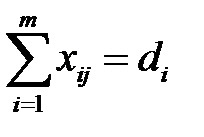
și în sensul problemei
Problema dietei. Necesară în dieta de zi cu zi m tipuri de substanțe nutritive conținute în n tipuri de produse.
aij - numărul de unități i-lea nutrient în unitatea j-a produsului;
numărul necesar de unități de nutrienți i-lea în dieta de zi cu zi - bi;
cj - valoarea unitară a produsului j-lea.
Provocarea este de a găsi achizițiile planului. minimizarea costului total:
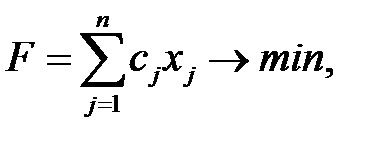
cu condiția ca fiecare nutrient va fi prezent în produsele achiziționate într-o cantitate nu mai puțin de dorit
și în sensul problemei. în cazul în care.
În problema încărcare a unei nave este necesară pentru a descărca diferite tipuri de mărfuri, astfel încât valoarea totală a acestora a fost cea mai mare.
j - tipul camerei de marfă;
n - numărul de tipuri de mărfuri;
b1. b2 - capacitatea și capacitatea unui compartiment de marfă a navei;
xj - numărul de unități de tip j-a de marfă, pe care am dori să se scufunde.
Provocarea este de a găsi un set. maximizarea valorii totale
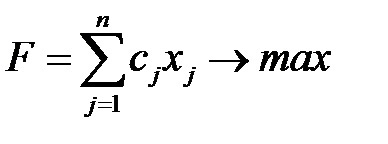
în conformitate cu constrângerile de capacitate și a capacității
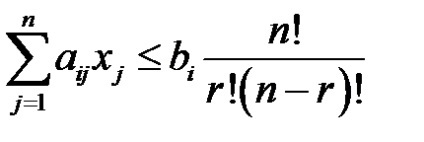
în cazul în care. xj - întregi.
Exemplu unui model matematic al problemei
EXEMPLUL №1.1. Crearea unui model matematic al problemei.
Pentru producția de mese de calculator I-st și II-lea tipuri necesită trei tipuri de resurse: lemn, plastic și forței de muncă. Cerințe de resurse pentru producerea unui tabel de fiecare tip, stocurile de resurse, precum și profitul din vânzarea unui tabel din fiecare specie sunt date în tabelul 1.1.:
Tabelul 1.1. - date de referință
Unitate de produs de tip I-lea
Unitatea de producție de tip II-lea
Necesitatea de a găsi un plan pentru a elibera produsul, permite să se obțină cel mai mare profit.
Să x1 și x2 - numărul de produse I-st și tipul II-lea, respectiv.
Condițiile de - limită pentru fiecare produs trebuie să fie după cum urmează: din moment Planul de ieșire ar trebui să fie în intervalul de trecere disponibile, debitul fiecărui tip de resursă ar trebui să nu mai fie decât limita stabilită, sau limita strict.
condiție - limita pe un copac este după cum urmează:
,
condiție - restricția pe material plastic:
,
condiție - limită privind costurile forței de muncă:
.
În plus, x1 variabila. x2 trebuie să fie mai mare sau egală cu zero:
.
Câștig din vânzarea de produse este:
pentru că profit ar trebui să fie maxim, este necesar să se găsească maximă a funcției obiectiv.
Modelul matematic al problemei este după cum urmează:
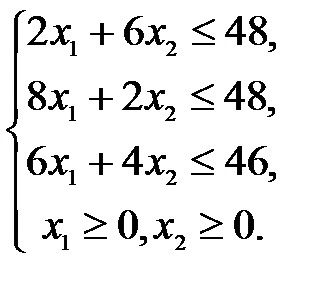
După calcularea modelului matematic (decizia ei) sunt determinate de x1 valoare. x2. satisfacerea constrângerilor de sistem și oferind un maxim al funcției obiectiv, și anume, calculat cantitatea fiecărui tip de produse necesare pentru a obține profitul maxim dintr-o anumită stocuri de resurse.
EXEMPLUL №1.2. Crearea unui model matematic al problemei.
Fabrica produce două tipuri de săpun: rufe și toaletă. Produsele ambelor tipuri merge la en-gros. Pentru producerea celor două ingrediente utilizate săpun - A și B. maxime posibile Stocurile diurn ale acestor ingrediente sunt 6 m și 8 m, respectiv. Costurile cunoscute ale ingredientelor A și B la 1 t săpunurile corespunzătoare (Tabel. 1.2.). Studiind piață a arătat că cererea de zi cu zi pentru săpun niciodată nu depășește cererea pentru săpun timp de mai mult de 1 tona. În plus, sa constatat că cererea de săpun nu depășește 2 tone pe zi. Prețul en-gros de o tonă de săpun este de 3 mii. Frecați. și o tonă de săpun - 2 mii ruble ..
Tabelul 1.2. - date de referință
Curgerea ingrediente ingr t. / Săpun T
Rezerva, că Ingram. / Noapte