circuit design Calculat
1) Dimensiunile fasciculului transversale sunt mult-corp mai mică decât lungimea (fascicul de suprapunere)
2) Placă-corp, unul dintre p-s, care este mult mai mică decât celelalte (interval de două suprapuse, în partea de jos-beam I)
3) delimitată de carcasa-corp suprafețe curbe, distanța dintre care este mult mai mică decât raza de curbură (clădiri Dome, ziduri si rezervoare de pereti)
4) array-corp, toate dimensiunile de același ordin (platină și suport punte)
forțe externe, interne
Ei au numit forțe externe care acționează asupra corpului de către alte organisme. Acestea sunt împărțite în lumped și distribuite.
F- forță concentrată (kN)
Perechea de forțe me-, un cuplu (kN · m)
q- sarcină distribuită neuniform (kN / m)
Ei au chemat forțele interne generate în interiorul corpului prin acțiunea forțelor externe.
forțele interne aranjate haotic poate fi adus la vectorul principal și punctul principal.
Luați în considerare un lemn cu o aplicare haotică a forțelor externe F1, F2, F3, F4
1) În cadrul secțiunii lemn de susținere perpendicular pe axa tijei, care împarte unda noastră în 2 părți A și B
2) Se elimină o parte (partea A)
3) Piesele eliminate înlocuiesc factorii interne de putere a 6-
4) formează echilibrul ecuațiile de 6
a. Σh = 0 → N
b. Σy = 0 → Qy
c. Σz = 0 → Qz
d. ΣMx = 0 → Mx
e. ΣMy = 0 → My
f. ΣMz = 0 → Mz
Dacă oricare dintre factorii interni de forță va fi negativ, ar trebui să-l schimbe în direcția opusă dată.
secțiuni momente statice
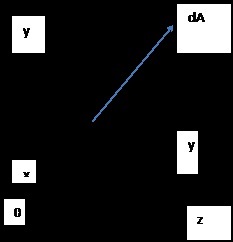

YDA - zona de timp elementar în ceea ce privește Oz
ZDA - zona elementar timp relativ Oy
momente statice în jurul axelor y și z sunt numite integralele
S - momentul static (cm3)
Sz = y∫dA ∫ydA
Sy = z∫dA ∫zdA
Aspecte statice pot fi negativ, pozitiv sau zero.
momentul static unei figuri complexe este suma momentelor statice ale componentelor sale simple.
Momentele de inerție
Distinge momentelor axiale, centrifugale polare de inerție.
Momentele de inerție axial este integrala: Iz = ∫y 2 dA
Iy = ∫z 2 dA (4 cm)
Polar integrală inerție este integrala: I # 421; = ∫ # 421; ²dA
inerție centrifug este integrala: Dyz = ∫zydA
Inerția centrifugă poate fi pozitivă, negativă și zero.
momente polare și de inerție axial, poate fi pozitiv numai.
Momentele de inerție ale secțiunilor elementare.
Iz = bh 3/12 Iz = bh 3/36 Iz = Iy = πd 4/64 Iy = πd 4/128
Iy = hb 3/12 Iy = hb 3/36 A = πd 2/2 Iy = hb³ / 36Iz = πd # 8308; / 128 Iz1 = 0.11r 4
Momentele de inerție în jurul axelor paralele
Dacă Sz și Sy = 0, formula ia forma:
Iy # 8321; = Iy + b²A - transfer paralel cu formula
Momentul de inerție în raport cu axele paralele, este egal cu suma momentului de inerție se referă axa centrală și produsul S (pătrat) bucăți pe distanța pătratică dintre aceste axe.
Axa principală momentele principale de inerție
Axele despre care momentele de inerție axial au o valoare extremă, iar momentele centrifuge = 0, numit axele principale de inerție. Poziția axelor principale de inerție este definită prin: tg # 8322, # 945; = - 2Dyz / Iz-Iy
unghi pozitiv # 945; întârziat din axa z în sens invers acelor de ceasornic, când axa principală trece prin centrul de greutate al secțiunii transversale, axele sunt numite axele centrale principale.
momentul de inerție axial se referă în principal centru axe sunt numite momentele principale de inerție și sunt calculate conform formulei.
1) Ipoteza continuității: presupune că materialul umple întreaga sumă prevăzută pentru el
2) Ipoteza de uniformitate și izotropie: implică faptul că proprietățile materialului sunt identice în toate punctele și direcțiile
3) Ipoteza elasticitate ideală: implică faptul că materialul este recupereaza complet forma după ce sarcina este îndepărtată
4) Ipoteza relației liniare dintre stres si tulpina: presupune că tensiunea este direct proporțională cu tulpinile
5) Ipoteza de deformare este mică: presupune că deformarea (rezidual) sunt mici în comparație cu dimensiunile corpului, și pot fi neglijate
Atunci când structurile de proiectare trebuie să aibă dimensiunile secțiunii transversale, astfel încât acestea să nu depășească așa-numitul, calificarea. distinge:
# 963; tensiuni normale adm admisibile
# 964; adm - forfecare admisibile
# 963; adm luate pentru materiale fragile, ca parte din rezistența maximă. # 963; adm = # 963; l / n1
Pentru materialele plastice pentru o parte din efortul de curgere: # 1004; # 1006 .adm; t / n # 8322;
n # 8321; și n # 8322, coeficientul de marjă de siguranță (și mai mare decât 1)
# 1006; adm = (0,5-0,6) # 1004; adm
calculele de rezistență
1. Determinarea tensiunii. puterea Verificați
2. Determinarea mărimii secțiunii transversale
3. Determinarea sarcinii admisă
Method parametrii inițiali
Dezavantajul metodei de integrare directă este necesitatea de a identifica un număr mare de constante arbitrare.
În cazul în care fasciculul este n-sectiuni, este necesar să se creeze și de a rezolva un sistem de ecuații algebrice 2n.
În metoda parametrilor inițiali, indiferent de cât de multe stații ar trebui să identifice două constante arbitrare.
E - modulul de elasticitate
Iz - moment de inerție Oz
# 965; - deformarea în punctul
# 965; 0 - deformarea inițială
# 952; a - unghiul inițial de rotație
x - distanța de la grindă la secțiunea avută în vedere
Constantele de integrare sunt aici înțeles simplu: este inițial (x = 0), valorile funcției necunoscute și derivații săi. Prin urmare, metoda de integrare ecuații diferențiale bazate pe formula, și este utilizat pe scară largă în mecanică structurală, numită metoda parametrilor inițiali.
Conform metodei parametrilor inițiali, fasciculul este împărțit în secțiuni. Substituind (12.38) la (12,39), obținem funcția devierile pe porțiunea grindă I:
Metoda diferențelor finite
Deformarea grinzilor elementare
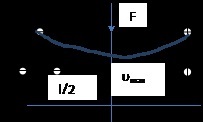
Cu o etanșeitate de:
Stânga - etanșare; dreapta - forță descendentă; deformare - mișcări netede de la 0 la sigilarea Strength.
Stânga - etanșare; peste tot - o sarcină distribuită uniform; deformare atât a forței - o tranziție lină în jos.
grinzi secțiune raționale
Motivul este o secțiune care are cea mai mare putere și economie.
In cele mai multe tensiuni normale de îndoire apar în locuri mai îndepărtate de axa z.
Mai aproape de Oz, tensiunea normală este mai mică, iar pe axa, acestea sunt egale cu zero
Și cu materialul: cantitatea cea mai mare ar trebui să se concentreze mult mai puțin.
Astfel se obține o secțiune transversală în formă de I, care servește pentru percepția tensiunilor normale, iar peretele servește pentru a conecta rafturile și percepția tensiunilor tangențiale, care rezultă din acțiunea forțelor de forfecare.
Fasciculul de rezistență uniformă
RSB se numește o grindă secțiune transversală, care are tensiunile maxime în toate secțiunile sunt identice și sunt permise
Formular RBS se determină din formula:
Offset (felie). concepte de bază
Shift (cut) - forma statului deformat-stres, în care numai un factor de putere internă are loc în secțiune transversală.
Forfecare (cut) se calculează zagaze sudate etc.
apar la forfecare forfecare secționate
Q - forță transversală; A - aria secțiunii transversale
punctele de intersecție periculoase
Pericolele din punctul cel mai îndepărtat de linia neutră
Pentru definirea lor prin toate punctul extrem al secțiunii pentru a menține linia paralelă neutru
Cel mai îndepărtat de NL va trece printr-o secțiune periculoasă a punctului
circuit design Calculat
1) Dimensiunile fasciculului transversale sunt mult-corp mai mică decât lungimea (fascicul de suprapunere)
2) Placă-corp, unul dintre p-s, care este mult mai mică decât celelalte (interval de două suprapuse, în partea de jos-beam I)
3) delimitată de carcasa-corp suprafețe curbe, distanța dintre care este mult mai mică decât raza de curbură (clădiri Dome, ziduri si rezervoare de pereti)
4) array-corp, toate dimensiunile de același ordin (platină și suport punte)
forțe externe, interne
Ei au numit forțe externe care acționează asupra corpului de către alte organisme. Acestea sunt împărțite în lumped și distribuite.
F- forță concentrată (kN)
Perechea de forțe me-, un cuplu (kN · m)
q- sarcină distribuită neuniform (kN / m)
Ei au chemat forțele interne generate în interiorul corpului prin acțiunea forțelor externe.
forțele interne aranjate haotic poate fi adus la vectorul principal și punctul principal.
Luați în considerare un lemn cu o aplicare haotică a forțelor externe F1, F2, F3, F4
1) În cadrul secțiunii lemn de susținere perpendicular pe axa tijei, care împarte unda noastră în 2 părți A și B
2) Se elimină o parte (partea A)
3) Piesele eliminate înlocuiesc factorii interne de putere a 6-
4) formează echilibrul ecuațiile de 6
a. Σh = 0 → N
b. Σy = 0 → Qy
c. Σz = 0 → Qz
d. ΣMx = 0 → Mx
e. ΣMy = 0 → My
f. ΣMz = 0 → Mz
Dacă oricare dintre factorii interni de forță va fi negativ, ar trebui să-l schimbe în direcția opusă dată.
secțiuni momente statice


YDA - zona de timp elementar în ceea ce privește Oz
ZDA - zona elementar timp relativ Oy
momente statice în jurul axelor y și z sunt numite integralele
S - momentul static (cm3)
Sz = y∫dA ∫ydA
Sy = z∫dA ∫zdA
Aspecte statice pot fi negativ, pozitiv sau zero.
momentul static unei figuri complexe este suma momentelor statice ale componentelor sale simple.
Momentele de inerție
Distinge momentelor axiale, centrifugale polare de inerție.
Momentele de inerție axial este integrala: Iz = ∫y 2 dA
Iy = ∫z 2 dA (4 cm)
Polar integrală inerție este integrala: I # 421; = ∫ # 421; ²dA
inerție centrifug este integrala: Dyz = ∫zydA
Inerția centrifugă poate fi pozitivă, negativă și zero.
momente polare și de inerție axial, poate fi pozitiv numai.
Momentele de inerție ale secțiunilor elementare.
Iz = bh 3/12 Iz = bh 3/36 Iz = Iy = πd 4/64 Iy = πd 4/128
Iy = hb 3/12 Iy = hb 3/36 A = πd 2/2 Iy = hb³ / 36Iz = πd # 8308; / 128 Iz1 = 0.11r 4