Exemplul 1. Rezolvați sistemul de ecuații prin metoda Cramer
Mai întâi compunem și calculam principalul determinant al acestui sistem:
Întrucât, atunci sistemul are o soluție unică, care poate fi găsită prin regula lui Cramer:
unde sunt obținute din determinant prin înlocuirea coloanelor 1, 2 sau 3, respectiv cu coloana cu termeni liberi.
Deci, singura soluție.
Exemplul 2. Rezolvați sistemul de ecuații prin metoda Cramer
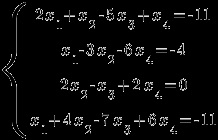
Să facem determinantul principal al acestui sistem:
Folosind proprietățile determinantului, noi creăm în prima coloană zerouri. Pentru a face acest lucru,
- A doua și a treia linie vor fi lăsate neschimbate,
- Multiplicați al doilea rând cu -2 și adăugați la primul rând
- Multiplicați al doilea rând cu -1 și adăugați la al patrulea
După aceste conversii, valoarea determinantului nu se schimbă, dar se va scrie în formularul următor
Acum, folosind definiția determinantului și extinderea acestuia asupra elementelor din a patra coloană, obținem:
Astfel, determinantul principal al sistemului de ecuații este diferit de zero. Prin regula lui Cramer, un astfel de sistem are o soluție unică. Să-l găsim. Pentru a face acest lucru, noi creăm și calculam încă patru determinanți:
În conformitate cu regula lui Kramer, avem o soluție:
Deci, singura soluție.