Sinusoidă. Curba plat caracterizează variația valorii sinusul unghiului în funcție de unghiul, numit o undă sinusoidală. Pentru a construi un sinusoid, cercul dat este împărțit în mai multe părți egale (figura 1). Pentru același număr de părți egale împărțiți axa sinusoidului, lungimea căreia este egală cu lungimea cercului 2nR. Din punctele de diviziune ridică până la perpendicularele axa pe care stabilesc ordinates egalează intervalele respective sinusurile. Punctele obținute I, II, III etc. sunt conectate printr-o curbă netedă. Dacă este necesar, curba poate fi continuată dincolo de punctul VIII. La construirea liniilor de șurub, întâlnite adesea în tehnologie, se utilizează un sinusoid comprimat, în care pasul este mai mic decât circumferința.
Fig. 1. Construirea unui sinusoid
Spiral. Curba plan care se obține atunci când punctul se deplasează, se rotește în jurul unui centru în timp ce se retrage din el potrivit unei legi, numit helix. Dacă distanța de la centru este proporțională cu deplasarea unghiulară a punctului, curba se numește spirala Archimedes. Dimensiunile curbei depind de magnitudinea pitch-ului spiralei OVIII (figura 2). Pentru a construi curba, trageți un cerc cu o rază egală cu pitchul spiral. Împărțiți pasul și cercul cu același număr de părți egale. De la centrul O, una, două, trei, etc., sunt depuse de-a lungul razei, obținându-se puncte ale spiralei I, II, III etc.
Curbele exprimate prin ecuații. Curbele regulate sunt adesea date de ecuații. Să presupunem, de exemplu, că trebuie să construim o curbă dată de ecuația x = y 2 + 2 (figura 3). Axele coordonatelor x și y sunt desenate. Substituind în ecuația pentru valori y: .. 0, 1, 2, 3, 4, etc. Găsiți ceea ce va fi egală cu valoarea lui x. În primul caz, x = 2, a doua x = 3, a treia - b, în a patra - .. 11, etc. reprezentate pe axele x și y cantități corespunzătoare și la intersecția perpendicularele sunt punctele I, II, III, IV, V și altele.
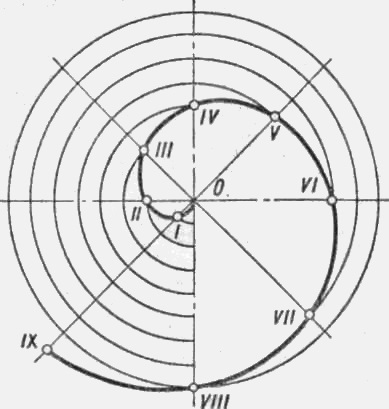
Fig. 2. Construirea spiralei Archimedes
Fig. 3. Construcția curbei din Eq.