Interpretarea geometrică a metodei acordurilor este după cum urmează
(Figura 6.2.3-8).
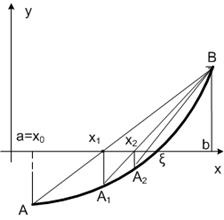
Desenați un segment de linie prin punctele A și B. O altă abordare x1 este abscisa punctului de intersecție al coardei cu axa 0x. Construim ecuația unui segment de linie:
Am setat y = 0 și găsim valoarea x = x1 (următoarea aproximație):
Repetăm procesul de calcule pentru a obține următoarea aproximație cu rădăcina - x2:
În cazul nostru (figura 6.2.11) și formula de calcul pentru metoda acordurilor vor avea forma
Această formulă este valabilă atunci când punctul b este luat ca punct fix, iar punctul a apare ca aproximație inițială.
Luați în considerare un alt caz (Figura 6.2.3-9) când.
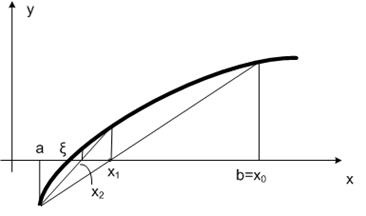
Ecuația liniei pentru acest caz are forma
Următoarea aproximație x1 pentru y = 0
Apoi, formula de recurență pentru metoda acordurilor pentru acest caz are forma
Se remarcă faptul că este selectată pentru o metodă de punct fix în segmentul coardei [a, b], care satisface condiția f (x) # 8729; f ¢ (x)> 0.
Astfel, dacă un punct este considerat a fi un punct fix, atunci x0 = b apare ca aproximație inițială și invers.
condiții suficiente care asigură calculul rădăcina ecuației f (x) = 0 de la formula coardele sunt aceleași ca și pentru metoda tangentă (metoda Newton), dar în schimb apropierea inițială este selectat un punct fix. Metoda este o modificare a coardele metodei Newton. Diferența constă în faptul că, în următoarea apropierea metodei Newton efectuează punctul de intersecție al tangentei la axa 0x și acorduri în metoda - punctul de intersecție cu coarda axa 0X - aproximări converg spre partea de sus din diferite direcții.
Estimarea erorii în metoda acordurilor este dată de
Condiția de terminare a procesului iterativ prin metoda chordului
În cazul în care M1 <2m1. то для оценки погрешности метода может быть использована формула | xn - xn-1 | £ e.
Exemplul 6.2.3-4. Specificați rădăcina ecuației e x - 3x = 0, separată pe intervalul [0; 1] cu o precizie de 10 -4.
Să verificăm condiția de convergență:
Prin urmare, pentru un punct fix ar trebui să aleagă o = 0, și ca o aproximare inițială a lua x0 = 1, deoarece f (0) = 1> 0 și f (0) * f „(0)> 0.
Rezultatele de calcul obținute utilizând formula
6.2.3-14, sunt prezentate în Tabelul 6.2.3-4.
Precizia necesară este obținută la a opta iterație. În consecință, pentru o valoare aproximativă a rădăcinii, putem lua x = 0.6191.
Algoritmul metodei chord este prezentat în Fig. 6.2.3-10.
Alegerea unui punct fix care determină tipul de formula de calcul se face prin compararea una dintre extremitățile intervalului [a, b] cu aproximare inițială (x0 = a). Pe măsură ce capătul fix al segmentului (punctul c) este selectat unul care nu coincide cu aproximarea inițială.
Fig. 6.2.3-10. Schema algoritmului metodei acordurilor