TEORIA LUCRĂRII: Suma unghiurilor triunghiului.
- Consolidarea și testarea cunoștințelor studenților pe tema: "Suma unghiurilor triunghiului";
- Dovada unghiurilor unui triunghi;
- Aplicarea acestei proprietăți în rezolvarea celor mai simple probleme;
- Utilizarea materialului istoric pentru dezvoltarea activității cognitive a elevilor;
- Pregătire de exactitate în desenele desenate.
- Verificați capacitatea elevilor de a rezolva probleme.
- triunghi;
- Teorema privind suma unghiurilor unui triunghi;
- Un exemplu de sarcini.
Fișier: O.gif Triangle rectilinie, o parte a planului delimitat de trei segmente de linie (laturi ale triunghiului (în geometrie)) având pairwise la un capăt comun (noduri de triunghi (geometrie)). Un triunghi ale cărui lungimi de toate laturile sunt egale se numește echilateral. sau corectă. Un triunghi cu două laturi egale este isoscele. Triunghiul se numește unghi ascuțit. dacă toate unghiurile sunt ascuțite; dreptunghiular - dacă unul dintre unghiurile sale este drept; obtuzã - dacã unul dintre colțurile sale este unghiular. Mai mult decât un unghi drept sau obtus Un triunghi (în geometrie) nu poate avea, deoarece suma celor trei unghiuri este egală cu două unghiuri drepte (180 ° sau, în radiani, p). Zona triunghiului (în geometrie) este ah / 2, unde a este fiecare parte a triunghiului, luată pentru baza sa, iar h este înălțimea corespunzătoare. Liniile triunghiului sunt supuse condiției: lungimea fiecăruia este mai mică decât suma și este mai mare decât diferența de lungime a celorlalte două părți.
Fișier: O.gif Triunghiul este cel mai simplu poligon cu 3 noduri (unghiuri) și 3 laturi; o parte a planului delimitată de trei puncte și trei segmente pereche care leagă aceste puncte.
Trei puncte de spațiu care nu se află pe o linie corespund unui singur avion.
Orice poligon poate fi împărțit în triunghiuri - acest proces se numește triangulare.
Există o secțiune a matematicii dedicată în întregime studiului regularităților triunghiulare - trigonometria.
Teorema privind suma unghiurilor unui triunghi.
Fișier: T.gif Teorema privind suma unghiurilor unui triunghi este o teoremă clasică a geometriei euclidane, afirmând că suma unghiurilor unui triunghi este de 180 °.
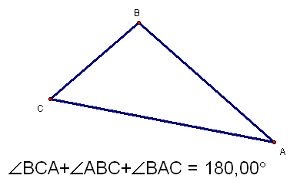
Lăsați ABC-ul să fie dat. Desenați o linie dreaptă paralelă cu (AC) prin vârful B și marcați punctul D pe ea astfel încât punctele A și D să se afle pe laturile opuse ale liniei BC. Apoi, unghiul (DBC) și un unghi (ACB) sunt ambele situată la liniile paralele crosswise interne AC și BD și un secantă (BC). Apoi, suma unghiurilor triunghiului la vârfurile lui B și C este egală cu unghiul (ABD). Dar, unghiul (ABD) și unghiul (BAC) la vârful triunghiului A ABC sunt interne cu linii paralele unilaterale AC și BD intersectări și (AB), iar suma lor este egală cu 180 °. În consecință, suma unghiurilor triunghiului este de 180 °. Teorema este dovedită.
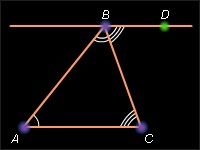
Colțul exterior al triunghiului este egal cu suma a două unghiuri ale triunghiului, nu adiacente acestuia.
Lăsați ABC-ul să fie dat. Punctul D se află pe AC astfel încât A se întinde între C și D. Atunci BAD - coltul exterior al triunghiului la apex A și A + BAD = 180 °. Dar A + B + C = 180 ° și prin urmare B + C = 180 ° - A. De aici BAD = B + C. Corolarul este dovedit.
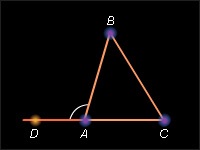
Colțul exterior al triunghiului este mai mare decât orice unghi al triunghiului care nu este adiacent acestuia.
Colțul exterior al triunghiului este un unghi adiacent unui anumit unghi al acestui triunghi. Dovediați că colțul exterior al triunghiului este egal cu suma a două unghiuri ale triunghiului care nu sunt adiacente acestuia.
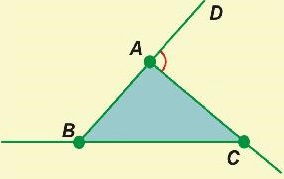
Lăsați în ABC ∠DAC - extern (figura 1). Apoi ∠DAS -∠VAS = 180 ° (prin proprietate unghiuri adiacente), teorema pe colțurile unei sume triunghi ∠V ∠S + = 180 ° -∠VAS. Din aceste egalități obținem ∠DAC = ∠B + ∠C
În geometria hiperbolică suma unghiurilor unui triunghi este întotdeauna mai mică decât 180. În geometria euclidiană este întotdeauna egal cu 180. În geometrie, suma Riemann unghiurilor unui triunghi este întotdeauna mai mare decât 180.
Din istoria matematicii:
Euclid (III în Î.H.) în lucrarea "Început" dă următoarea definiție: "Linile paralele sunt linii drepte care sunt în același plan și, fiind continuate în ambele moduri nelimitate, nu se întâlnesc unul cu celălalt" .
Posidonius (I în BC) "Două linii drepte situate în același plan, echidistant unul față de celălalt"
Gânditorul grec vechi Papp (III în BC) a introdus simbolul liniilor paralele - semnul =. Ulterior, economistul englez Ricardo (1720-1823) a folosit acest simbol ca semn egal.
Numai în secolul XVIII a început să folosească simbolul paralelismului liniilor drepte - simbolul ||.
Pentru o clipă legătura vie între generații nu este întreruptă, în fiecare zi învățăm experiența acumulată de strămoșii noștri. Grecii pe baza observațiilor și experiența practică pentru a trage concluzii exprimate ipoteza, atunci, oamenii de știință de la reuniuni - simpozioane (literalmente „sărbătoare“) - aceste ipoteze au încercat să justifice și să dovedească. La acea vreme, a existat o declarație: "Într-o dispută, adevărul se naște".
- Ce este un triunghi?
- Ce spune teorema cu privire la suma unghiurilor unui triunghi?
- Care este colțul exterior al triunghiului?
Lista surselor utilizate:
Deasupra lecției lucrate:
Puteți pune întrebarea despre educația modernă, puteți exprima o idee sau puteți rezolva o problemă urgentă la Forumul Educațional. unde la nivel internațional se adună un consiliu educațional de gândire și acțiune proaspătă. Prin crearea unui blog, nu numai că vă veți îmbunătăți statutul de profesor competent, ci veți aduce o contribuție semnificativă la dezvoltarea școlii viitorului. The Guild Leaders of Education deschide porțile pentru specialiștii de vârf și vă invită să colaboreze la crearea celor mai bune școli din lume.