Înainte de a începe formarea și gestionarea portofoliului de obligațiuni, este necesar să se prezinte principalii factori care influențează fluctuațiile prețurilor obligațiunilor.
Prețul curent de piață P 0 al unei obligațiuni care are plăți cupon pe an este determinat de formula:
unde i / m este randamentul până la maturitate; Ct / m plăți cupon; Denumirea Mmn; n este numărul de ani până la maturitatea obligațiunii.
Cu toate acestea, valoarea nominală a obligațiunilor unei clase este, în general, neschimbată, astfel încât impactul său asupra modificării prețului obligațiunii poate fi neglijat. Efectul acelorași plăți de cupoane și scadența asupra prețului obligațiunilor poate fi în cele din urmă redus la studiul impactului randamentului până la scadență.
În acest caz, sub volatilitatea (variabilitatea) prețului obligațiunii se înțelege reacția prețului obligațiunii la o schimbare instantanee, bruscă a randamentului său până la maturitate, cu alte lucruri fiind egale.
Reacția prețului obligațiunii la modificarea randamentului solicitat are o serie de trăsături caracteristice:
1) Relația dintre randamentul până la scadență i și prețul de piață al unei obligațiuni este inversată. În același timp, valoarea lui i crește # 8710; P 0 pentru aceeași scădere a randamentului la stingere # 8710; Sunt în creștere.
2) Pentru aceeași maturitate a obligațiunilor, cu cât este mai mare rata dobânzii la cupon, cu atât prețul obligațiunilor este mai scăzut și reacționează la aceleași modificări ale randamentului până la maturitate. În consecință, cu cât rata cuponului este mai mică, cu atât mai puternică este reacția prețului P 0 la aceleași variații ale randamentului la maturitate.
3) Dacă rata dobânzii cuponului nu se modifică, o creștere a maturității obligațiunii determină o reacție mai puternică a prețului obligațiunii P 0 la aceleași modificări ale randamentului până la scadență i.
4) Modificările mici ale randamentului până la maturitate conduc la modificări identice ale prețului obligațiunilor în ambele direcții. Cu alte cuvinte, dacă randamentul i crește cu o mică sumă, rezultă o reducere procentuală a prețului P 0, care este aproximativ egală cu creșterea procentuală a lui P0 cu aceeași scădere nesemnificativă i.
Prognoza este coloana vertebrală a oricărui sistem de tranzacționare, astfel încât, în mod competent, previziunile Forex vă pot face aspidi monetare.
5) Modificări semnificative de randament la maturitate i induce asimetrică reacție obligațiuni preț: dacă randamentul la maturitate a crescut cu un procent mic (de exemplu, 2%), atunci reducerea consecutivă a prețului de obligațiuni va fi procentul este mai mică decât valoarea absolută a procentului incrementului ratelor obligațiunilor la randamente mai mici la maturitate la aceeași 2%.
6) Pentru un anumit nivel de variație a randamentului până la maturitate # 8710; i, cu cât randamentul inițial până la scadență este mai mic, cu atât mai mare este răspunsul prețului la schimbări i.
Rezumând toate cele șase proprietăți ale volatilității prețului obligațiunilor, puteți observa că este puternic influențată de cinci factori:
a) nivelul randamentului până la maturitate;
b) intervalul de variație a randamentului până la maturitate;
c) direcția acestor modificări;
d) valoarea ratei cuponului;
e) maturitate.
Se acceptă în general că durata caracterizează "maturitatea medie" a întregului flux de plăți în numerar garantat de obligațiune. Makoli însuși a definit durata ca "timpul mediu ponderat pentru stingerea fluxurilor de numerar ale obligațiunii, unde" ponderile "sunt valorile actuale ale acestor fluxuri de numerar." Cu alte cuvinte, dacă momentele de timp t 1, t 2, t 3. tn sunt cunoscute. după care investitorul primește plăți cuponului C 1. C2, C3. C n și denumirea Mn. atunci durata este media ponderată a acestor intervale de timp pentru acțiunile din prețul Pi. care este plătită prin fluxul de numerar corespunzător (plata cuponului și valoarea nominală) la valoarea inițială P 0 a obligațiunii.
Durata oricărei obligațiuni se calculează prin formula:

În consecință, durata obligațiunilor cu cupon zero este întotdeauna egală cu scadența acestei obligațiuni de ani.
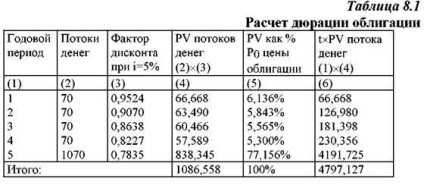
Este mai dificil de calculat durata legăturii cuponului. Să presupunem că un investitor dorește să determine durata de obligațiuni cu cupon valoarea nominală de 1.000 de ruble și o perioadă de 5 ani, cu un interes cupon de 7%, de plătit anual, iar randamentul la maturitate i = 5%. Prețul unor astfel de obligațiuni:
Pentru a calcula D, găsim factorii de discount și valorile actuale ale fluxurilor bănești furnizate de obligațiuni (în tabel, datele despre fluxurile de bani în ruble):

Proprietățile duratei. Durata depinde de următorii factori:
a) randamentul până la scadență;
b) scadența;
c) procentul plăților cuponului. De regulă:
Durata D a obligațiunilor cu cupon zero (pur scont) este întotdeauna egală cu scadența acestora;
obligațiuni cu cupon N D întotdeauna sub T. scadențelor În acest caz, în cazul în care amploarea plăților cuponului periodică rămâne neschimbată, cu creșterea maturitatea T = diferența NXT între lungimea D și perioada T este crescut.
# 9633; de regulă, pentru aceeași perioadă de scadență, obligațiunile D vor fi mai mici, cu atât valoarea plăților cuponului este mai mare (și invers). Această proprietate poate fi încălcată cu randament ridicat până la scadență i și cu o maturitate semnificativă;
P dacă valoarea plăților cupon Ct și randamentul la scadență i OS se topesc neschimbate, legăturile durată D sunt, în general, nonincreasing cu creșterea T. sale maturitate Relația pozitivă dintre valorile T și D se observă pentru toate legăturile cu excepția celor care au cea mai mare valoare i cu T. lung
La valori constante ale plăților cuponului Q și scadenței T,
cu atât randamentul până la scadență este mai mic i. cu atât este mai mare valoarea duratei D.
Valoarea [(D) / (1 + i)] este denumită, de obicei, durata modificată (MD). apoi:
variație procentuală P 0 ≈ MD x (% schimbare i) ( „minus“ semn indică faptul că variația cantităților i și Po este direcția inversă, i crește conduce la o scădere de cădere Po i. - pentru a crește Po).
Metoda de utilizare a duratei MD modificată pentru a evalua modificarea procentuală a prețurilor de obligațiuni cu fluctuații ale ratelor dobânzilor pe piață (care se vor reflecta în modificările randamentul la scadență) dă rezultate mai precise în cazul utilizării sale pentru relativ obligațiuni pe termen scurt cu plăți rată mare de cupon decât pentru obligațiunile pe termen lung cu un nivel scăzut plăți cupon.