Rezultatele măsurării diametrului capilarului sunt înregistrate în Tabelul 4.2, măsurătorile rămase în Tabelul 4.3.
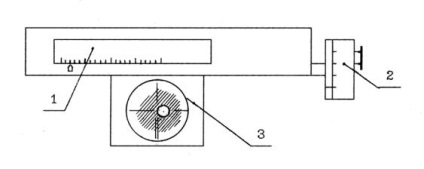
4.5.1 Măsurați diametrul capilarului cu un microscop. Pentru a face acest lucru, plasați cutoff-ul capilarului pe diapozitivul de microscop. Se potrivesc liniile de vizare ale micrometrului ocular la dreapta și apoi la marginea din stânga a deschiderii capilare, ca în figura 4.4. Luați eșantioane pe o scală orizontală (la milimetri întregi) și pe o scală de tambur (zeci și sute de milimetru). Găsiți diametrul capilarului ca diferență a acestor probe. Diametrul capilarului este măsurat în trei direcții diferite. Pentru diametrul capilarului, luați media aritmetică a rezultatelor obținute. Calculați raza R a capilarului.
Cu ajutorul greutăților, se determină masa m 1 a sticlei goale 4 cu o precizie de 0,01 g.
4.5.3 Măsurați înălțimea inițială a nivelului lichidului h 'din planul mesei folosind o riglă.
1 - scară orizontală; 2 - scara tamburului; 3 - câmp vizual al microscopului Figura 4.4 - Schema de măsurare a diametrului capilarului
4.5.4 capilar rapid omis din poziția A în poziția B (vezi. Figura 4.3), astfel încât fluidul picurată în paharul 4 și a porni cronometrul.
4.5.5 Se măsoară înălțimea h a capătului capilarului de la planul mesei.
4.5.6 Când lichidul din sticlă 4 este suficient (1/2 volum), opriți cronometrul ridicând rapid capilarul în poziția A. Citiți timpul de scurgere a lichidului din cronometru.
4.5.7 Se măsoară nivelul lichidului final h "în recipientul 1.
4.5.8 Se determină masa m 2 a paharului cu lichidul.
4.5.9 Se înregistrează în tabelul 4.3 valorile: accelerația datorată gravitației
(g = 9,8 m / s 2), densitatea lichidului (ρ de apă = 10 3 kg / m 3) și lungimea capilarului, a cărei valoare este indicată pe instalație.
5 Determinarea modulului Young în deformarea tulpinii
Scopul lucrării este de a studia comportamentul corpurilor deformate sub acțiunea forțelor externe și de a determina experimental modulul Young în deformarea tulpinilor.
5.2 Introducere teoretică
In mecanica teoretică (staticii) a studiat echilibrul unui corp rigid; această idee a materialului este suficientă pentru a rezolva problema statică - determinarea condițiilor în care posibilitatea de echilibrare reciprocă a forțelor aplicate corpului. Când studiază rezistența materialelor la acțiunea acestor forțe, o idee aproximativă brută despre proprietățile materialului nu mai este suficientă; trebuie să ținem cont de faptul că nu există corpuri absolut solide în natură.
În realitate, organismele sub acțiunea forțelor care le sunt aplicate într-o anumită măsură își schimbă forma și mărimea, adică ele sunt deformate. Mărimea și natura deformărilor sunt legate de structura și structura materialelor utilizate de noi. Toate aceste materiale pot fi împărțite în două clase: cristaline și amorfe [1].
Materialele cristaline constau dintr-o cantitate uriașă de cristale mici împrăștiate una peste cealaltă. Se știe că într-un cristal separat (cristal unic) atomii sunt aranjați într-o anumită ordine, formând o latură de cristal. Structura cristalină are metale (corpuri policristaline). În corpurile amorfe (sticlă, rășini etc.), spre deosebire de cristale, nu există o ordine strictă în aranjarea atomilor. Numai cei mai apropiați atomi vecini sunt aranjați într-o anumită ordine Dar repetabilitate strictă în toate direcțiile unuia
și același element structural care este caracteristic pentru cristale, nu există corpuri amorfe.
Atomii sunt ținute în echilibru de forțele de interacțiune. Deformarea corpurilor apare datorită schimbărilor în aranjamentul atomilor, convergenței lor sau îndepărtării lor. Deformațiile sunt împărțite în elastic și plastic. Deformările elastice sunt acele schimbări în forma și mărimea elementelor care dispar după îndepărtarea forțelor care le-au provocat - corpul își restabilește complet forma anterioară. Aceste deformații sunt legate numai de distorsiunile elastice ale rețelei de atomi. Experiența arată că se observă deformări elastice, în timp ce magnitudinea forțelor externe nu depășește o anumită limită.
Dacă forțele externe au depășit această limită, atunci ca rezultat al deplasării, atomii și moleculele își schimbă "vecinii" și încep să interacționeze cu
altele. După încetarea forțelor externe, ele nu se mai întorc la poziția lor anterioară, forma și dimensiunile elementului nu sunt restabilite în forma lor originală. Astfel de deformări se numesc deformări plastice. Deformările plastice rămân în corp după ce încărcătura este îndepărtată, deci sunt numite și reziduale. În materialele cristaline, aceste deformări sunt asociate cu deplasările ireversibile ale unor straturi ale rețelei cristaline față de altele.
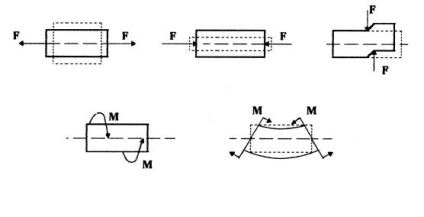
În funcție de direcția forțelor aplicate corpului, pot apărea diferite tipuri de deformare: tensiune, compresiune, forfecare, torsiune, îndoire. Vom lua cunoștință de deformarea corpurilor celei mai simple forme. Astfel de corpuri includ așa-numitele tije prismatice cu o axă dreaptă. În plus, presupunem că tijă în sine nu are nici o masă.
a - întindere; b - compresie; c - schimbare; r este torsiune; d - îndoire Figura 5.1 - Tipuri de deformări
întindere sau deformare la compresiune poate avea loc atunci când forțele exterioare sunt orientate de-a lungul unei linii drepte (de-a lungul axei tijei) în direcții diferite, așa cum se arată în figura 5.1, a b,. Dacă forțele externe acționează asupra tijei, care tind să se miște o parte din ea față de cealaltă, apare o deformare de forfecare. Astfel, așa cum se vede în figura 5.1,, formează o pereche de forță cu un umăr mic în axa longitudinală a planului tijă. Dacă tija este sub sarcină, a crea perechi opuse de forțe în planuri perpendiculare pe axa longitudinală a tijei, deformarea torsiune apare, prezentată în Figura 5.1 g. Și, în sfârșit, în cazul în care cele două perechi de forțe semne opuse acționează în planul axei longitudinale a tijei, deformarea îndoire este generată, așa cum se arată în figura 5.1, d.
În teoria elasticității, se demonstrează că toate tipurile de deformații pot fi reduse (cu condiția să fie suficient de mici) la deformarea simultană a întinderii (sau comprimării) și forfecării.
Deplasarea atomilor în deformarea unui material sub acțiunea forțelor externe este însoțită de o schimbare a forțelor de interacțiune dintre atomi - forțele de atracție și repulsie. În orice corp solid, sub acțiunea forțelor exterioare, apar forțe interne suplimentare,
formarea de materiale. Aceste forțe interne rezistă dorinței forțelor externe de a distruge corpul, de a-și schimba forma, de a separa o parte de cealaltă. Ei tind să restabilească vechea formă și dimensiunea părții deformate a corpului. Din aceasta rezultă că, pentru a rezolva problemele de rezistență a materialelor, trebuie în primul rând să învățăm din forțele externe să determinăm forțele elastice interne. Pentru aceasta, se utilizează metoda secțiunii transversale. a cărui esență este după cum urmează.
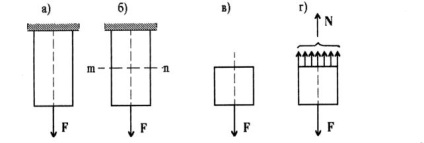
Lăsați forța F să fie aplicată la capătul tijei omogene, cu suprafața secțiunii transversale S acționând uniform pe toată secțiunea transversală a tijei, celălalt capăt al tijei fiind fixat, așa cum se arată în figura 5.2, a.
Să divizăm mental tijă în două părți prin secțiunea m-n, perpendicular pe axa sa, ca în figura 5.2, b, și să determinăm forțele cu care aceste părți ale tijei acționează reciproc. Deoarece ambele părți ale tijei sunt în echilibru, suma vectorială a forțelor care acționează asupra fiecăruia trebuie să fie zero. Părăsim partea superioară și luăm în considerare echilibrul inferior (vezi Figura 5.2, c, d). Echilibrul acestei părți nu este încălcat decât în cazul în care se vor aplica reacții - înlocuirea forțelor interne
Fiecare corp rigid dă deformări care respectă legea lui Hooke doar până la o anumită limită. Luați în considerare comportamentul materialelor în testul de tracțiune până la distrugere. Rezultatele măsurătorilor pot fi vizualizate cel mai clar sub forma unei așa-numite diagrame de întindere. La plotarea diagramei de-a lungul axei verticale, sarcinile sunt așezate într-o anumită scară, iar de-a lungul scalei orizontale - prelungiri absolute. Atunci când eșantionul este întins dintr-un material plastic (de exemplu, oțel moale), diagrama are forma prezentată în figura 5.4.
Secțiunea rectilinie OA corespunde deformărilor elastice ale eșantionului. Ordonata F A este valoarea forței de tracțiune care corespunde limitei de proporționalitate a lui P, adică cu cea mai mare tensiune, a cărei depășire provoacă o abatere de la legea lui Hooke.
Pe măsură ce forța de tracțiune este mărită dincolo de valoarea F A, deformarea începe să crească mai repede decât sarcina - diagrama are o formă curbilinie cu o convexitate în sus. Cu toate acestea, înainte de punctul B, deformările sunt elastice, adică eșantionul își recuperează forma după îndepărtarea încărcăturii. Dincolo de punctul B apar deformări inelastice.
Stresul, atunci când depășește o deformare în corp, se numește limita elastică σ y; în diagramă, sarcina care determină această tensiune este măsurată de către ordonata F B.
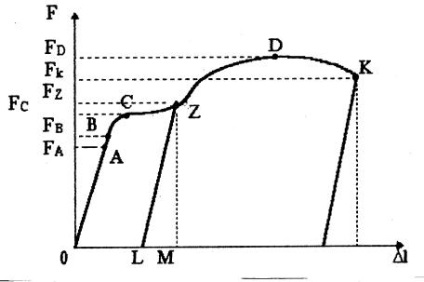
Punctele A și B sunt atât de apropiate una de cealaltă încât consideră că limita elastică și limita proporționalității sunt egale. Prin urmare, se spune adesea că materialul urmează legea lui Hooke până când atinge limita elasticității, deși ar fi mai corect să spunem - limita proporționalității.
Figura 5.4 - Diagrama de întindere a oțelului ușor
La o anumită valoare a forței de tracțiune F, materialul "curge"; Pentru a crește deformarea, este aproape inutil să creșteți forța de tracțiune. Diagrama formează o platformă orizontală (sau aproape orizontală).
Stresul la care are loc un astfel de flux de material - creșterea deformațiilor la o sarcină constantă (aproximativ), se numește punctul de randament σ m.
După formarea punctului de turnare, materialul din nou începe să reziste la extinderea ulterioară și pentru a mări alungirea l este necesară creșterea forței. Punctul D al diagramei corespunde celei mai mari valori a sarcinii.
Dacă sarcina este îndepărtată într-o stare descrisă de un anumit punct Z situat între punctele C și D, atunci când descărcarea diagramei va fi reprezentată de o linie dreaptă ZL, aproximativ paralelă cu linia dreaptă OA. Astfel, eșantionul în acest caz nu va reveni la dimensiunile sale inițiale; segmentul LM va reprezenta o alungire elastică, care încă variază proporțional cu sarcina cu modulul anterior de elasticitate; segmentul OL - alungirea reziduală și alungirea totală a segmentului OM la sarcina F z.
Cea mai mare valoare a tijei forței de tracțiune este reprezentată de ordonata F D; se numește adesea o sarcină distructivă. deoarece neob-