Brancharea (partiționarea setului G în subseturi). Am stabilit
8. Finitudinea algoritmului. Finitețea algoritmului rezultă din finiteitatea mulțimii G.
Prin metoda ramurilor și a limitelor se înțelege un algoritm pentru rezolvarea unei probleme care are o structură arborescentă pentru găsirea soluției optime și utilizarea rezultatelor rezolvării problemelor de evaluare. O structură arborescentă este numită în mod obișnuit un arbore.
Eficiența algoritmului de ramuri și limite este determinată de numărul de probleme rezolvate. Soluția problemei constă în două etape principale. În prima etapă este soluția optimă (sau aproape de ea). A doua etapă demonstrează optimitatea soluției obținute. A doua etapă, de regulă, este mai intensă decât prima. Aceasta înseamnă că numărul de sub-sarcini care pot fi rezolvate înainte de obținerea optimului poate fi semnificativ mai mic decât numărul de subprobleme care pot fi rezolvate pentru a dovedi optimitatea.
2. Afirmația problemei vânzătorului de călătorie
Problema clasică a agentului de vânzări (ZK) este formulată după cum urmează: există un graf complet orientat ponderat fără bucle G cu set de vârfuri N =; greutățile tuturor arcurilor nu sunt negative; în acest grafic este necesar să găsim ciclul Hamiltonian de greutate minimă.
Informația inițială despre ZK este considerată a fi reprezentată ca o matrice cu dimensiunea nxn. S =, unde sij este greutatea arcului (i, j) al graficului G, i =. j =. i ≠ j; toate elementele principalei diagonale a matricei S sunt zero.
Într-o interpretare tipică, nodurile 1, 2, ..., n din graficul G sunt orașe. Arcele reprezintă tranziții elementare posibile. Salesman, situat inițial în 1, aveți nevoie pentru a obține în jurul valorii de restul orașului, vizitând fiecare dintre ele exact o dată, și apoi să se întoarcă în oraș 1. Ponderile arcelor graficului sunt interpretate ca lungimea tranzițiilor elementare corespunzătoare. Este necesar să se găsească o lungime minimă de deplasare a rutei de călătorie care este admisibilă (adică satisfacerea cerințelor impuse). Luând în considerare alte interpretări posibile, cerința de simetrie nu este impusă matricei S, iar inegalitatea triunghiului nu este considerată obligatorie.
3. Problema vânzătorului călător prin metoda de programare dinamică
Prin metoda ramurilor și a limitelor se înțelege un algoritm pentru rezolvarea unei probleme care are o structură arborescentă pentru găsirea soluției optime și utilizarea rezultatelor rezolvării problemelor de evaluare. O structură arborescentă este numită în mod obișnuit un arbore.
Unul dintre algoritmii principali pentru rezolvarea ZK se bazează pe principiul programării dinamice. Prezentând acest algoritm, vom adera la terminologia corespunzătoare interpretării tipice a problemei.
Să fiu un oraș arbitrar (i # 206; N) și V este orice subset de orașe care nu conține orașul 1 și orașul i. Indicăm prin M (i, V) setul de căi, fiecare dintre care începe în orașul i, se termină în orașul 1 și trece ca intermediar numai prin orașele din setul V, intră fiecare într-o singură dată. Denumim cu B (i, V) lungimea celei mai scurte căi a setului M (i, V). Pentru rezolvarea problemei, B (i, V) este funcția Bellman. Așa cum este evident, B (1,) este lungimea minimă necesară a unei căi simple (fără auto-intersecții) închise care trece prin toate orașele.
Dacă V este un set singleton, V =, unde j ≠ 1 și j ≠ i, atunci setul M (i, V) constă dintr-o singură cale μ = (i, j, 1). prin urmare
eu # 206; N, j # 206; , j ≠ i (1.1)
Să presupunem că valorile funcției B (i, V) pentru toate i # 206; N \ și toate elementele posibile k (k Ecuațiile (1.1) - (1.12) sunt relații recurente de programare dinamică pentru rezolvarea problemei de călătorii de călător, oferind realizarea metodei inverse Bellman. Complexitatea computațională a problemei este egală cu, unde C este o constantă arbitrară (C> 0), n este numărul de orașe. Exemplul 1.1 Rezolvarea problemei vânzătorului călător, definită de matrice: În primul rând, folosind formula (1.1), determinăm valorile lui B (i,): În (2) = 5 + 6 = 11; În (3,) = 2 + 2 = 4; În (4) = 5 + 2 = 7; În (2,) = 2 + 1 = 3; În (3,) = 1 + 1 = 2; În (4) = 4 + 6 = 10. Mai departe, conform (1.2), obținem succesiv (pe partea stângă a fiecărei egalități scrise mai jos, se aleg acele valori ale parametrului j pe care se realizează minimul specificat pe partea dreaptă a (1.2)): În (2,) = min [s23 + B (3,); s24 + B (4)] = min (5 + 2; 2 + 10) = 7; În (3) = min [s32 + B (2,<4>); s34 + B (4,<2>)] = min (2 + 3; 1 + 7) = 5; În (4) = min [s42 + B (2,<3>); s43 + B (3,<2>)] = min (5 + 1; 4 +4) = 8; = min (4 + 7, 3 + 5, 4 + 8) = 8. Astfel, valoarea optimă a criteriului din exemplul examinat este de 8. Selecția efectuată vă permite să determinați traseul optim. Este după cum urmează: Pentru a scrie relațiile prin care se realizează metoda Bellman directă, introducem notația nouă. Fie M '(V, i) setul de căi, fiecare dintre care începe în orașul 1, trece ca intermediar numai prin orașele din subsetul V, intră fiecare într-o singură dată și se termină în orașul i; aici, ca și înainte, i este un oraș arbitrar (i # 206; N) și V este orice subset de N care nu conține orașe 1 și i. Lungimea celei mai scurte căi a mulțimii M '(V, i) este notată cu B * (V, i). Așa cum este evident, B * (, 1) este lungimea minimă necesară a unei căi simple (fără auto-intersecții) închise care trece prin toate orașele. Dacă V este un set singleton, V =, unde j ≠ 1 și j ≠ i. atunci mulțimea M '(V, i) constă în calea unică μ = (1, j, i). prin urmare Să presupunem că valorile funcției B * (V, i) pentru toate i # 206; N și toate elementele posibile k (k Ecuațiile (1.3) - (1.4) reprezintă relațiile de recurență a programării dinamice pentru rezolvarea problemei clasice de vînzător care călătoresc, care asigură realizarea metodei Bellman directe. Exemplu 1.2 Folosind metoda de numarare directa, rezolvati problema vandatorului care calatoreste definita de matrice: (rețineți că matricea S din acest exemplu este aceeași ca în cea precedentă). În primul rând, folosind formula (1.3), determinăm valorile lui B * (, i): B * (, 3) = 4 + 5 = 9; B * (, 2) = 3 + 2 = 5; B * (, 2) = 4 + 5 = 9; B * (4) = 4 + 2 = 6; B * (, 4) = 3 + 1 = 4; B * (, 3) = 4 + 4 = 8. În plus, conform formulei (1.4), obținem succesiv (în partea stângă a fiecărei egalități scrise mai jos, acele valori ale parametrului j sunt selectate pe care se realizează minimul din partea dreaptă a lui (1.4)): B * (, 4) = min [B * (, 3) + s34; B * (, 2) + s24] = min (9 + 1, 5 + 2) = 7; B * (, 3) = min [B * (, 4) + s43; B * (, 2) + s23] = min (6 + 4; 9 + 5) = 10; B * (, 2) = min [B * (, 4) + s42; B * (, 3) + s32] = min (4 + 5; 8 + 2) = 9; Astfel, valoarea optimă a criteriului din exemplul examinat este de 8. Selecția efectuată vă permite să determinați traseul optim. Este după cum urmează: Un alt algoritm de rezolvare a problemei vânzătorului călător este metoda de ramuri și limite. În esență, aceasta este o modificare a căutării complete a soluțiilor, optimizată de faptul că seturile de căutare neoptimale sunt întrerupte în funcție de anumite criterii. Formal, un arbore de variante este construit, pornind de la rădăcină. În rădăcină, este necesar să se dea o limită superioară și inferioară. Apoi ne ramurăm. Cu cât fragmentul arborelui va fi mai mic, cu atât mai mult succes a fost modul de funcționare a ramurii și a graniței. Următoarele definiții sunt valabile: Recordul actual este cel mai mare dintre estimările mai mici obținute în procesul de implementare. Topul este numit mort dacă scorul maxim din el nu depășește înregistrarea curentă. Este inutil să realizăm o ramificare suplimentară în ea. Un terminal este un vârf în care limitele superioare și inferioare coincid. Vârful, care a fost deja ramificat, este numit închis. Vertexele care nu sunt moarte, terminale sau închise, sunt numite deschise. Mai multe ramificații se fac în ele. Soluția se termină atunci când nu există noduri deschise în arborele nostru de opțiuni. Cea mai bună soluție este înregistrarea curentă. Limita superioară este determinată folosind algoritmul "lacom". Un algoritm lacomă este un algoritm pentru găsirea celei mai scurte distanțe prin alegerea celei mai scurte margini care nu a fost încă selectată, cu condiția să nu formeze o buclă cu marginile deja selectate. "Greedy" acest algoritm este numit pentru că în ultimii pași este necesar să plătiți brutal pentru lăcomie (ultima coaste, de regulă, este cea mai mare sau aproape de ea în lungime). Strategie: "Du-te la cel mai apropiat (care nu a intrat încă) orașul." Luați în considerare, de exemplu, rețeaua din Fig. 2, reprezentând un romb îngust. Lăsați vânzătorul care călătorește să înceapă de la orașul 1. Algoritmul "mergeți la cel mai apropiat oraș" îl va duce în orașul 2, apoi 3, apoi 4; la ultima etapă va trebui să plătiți pentru lăcomie, întorcându-vă de-a lungul diagonalei lungi a rombului. În consecință, nu va fi cel mai scurt, dar cel mai lung turneu. Pentru a calcula limita inferioară, mai întâi sumăm elementele minime pe rânduri și coloane și apoi alegem cea mai mare dintre sumele obținute, dar trebuie să luăm în considerare conflictul. Exemplul 2.1 Rezolvarea prin metoda sucursalelor și limitelor problemei vânzătorului călător, definită de matrice:
4. Problema vânzătorului de către sucursală și metoda limită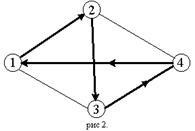

1. Calculăm limitele superioare și inferioare din rădăcină:
Estimarea superioară este calculată folosind așa-numitul algoritm "lacom": fiecare tranziție se face de la curent la cel mai apropiat oraș. Urmați traseul:
1 ® 2 ® 4 ® 3 ® 5 ® 1
Costul total al acestei rute este de 12, determină estimarea de top la rădăcină.
Pentru a calcula limita inferioară, mai întâi însumăm elementele minime pe rânduri și pe coloane, iar apoi din sumele obținute alegem cea mai mare:
Pe linii: 2 + 1 + 2 + 2 + 2 = 9
Coloanele: 2 + 2 + 3 + 1 + 2 = 10
Alegeți maximul valorilor și alegeți 10.
Să analizăm coloanele: putem trece la 2 (conflict). Prin urmare, limita inferioară este 10 + 2 = 12.
Ca urmare a rezolvării problemei, nu trebuie să ne dezvoltăm mai departe. Vom scrie traseul optim pentru vânzătorul care călătoresc:
Astfel, problema este rezolvată.
Practica generează tot mai multe probleme de optimizare, iar complexitatea lor crește. Sunt necesare noi modele și metode matematice care iau în considerare existența mai multor criterii, realizează o căutare globală a optimului. Cu alte cuvinte, viața ne obligă să dezvoltăm aparatul matematic de optimizare.
Aplicațiile reale ale optimizării discrete sunt foarte complexe. Metodele moderne de optimizare nu se confruntă întotdeauna cu rezolvarea problemelor reale fără ajutor uman. Nu, atâta timp cât există o teorie care ia în considerare toate caracteristicile funcțiilor care descriu formularea problemei. Ar trebui să se acorde prioritate metodelor care sunt mai ușor de gestionat în procesul de rezolvare a problemei.
Lista surselor utilizate
1. Bellman, R. Programarea dinamică - M. IL, 1960.- 400 p.
2. Bellman, R. Probleme aplicate ale programării dinamice - M. Nauka, 1965. - 457 p.
4. R. Bellman, S. Dreyfus Probleme aplicate ale programării dinamice - M. 1965 460 p.
Brancharea (partiționarea setului G în subseturi). Am stabilit
Informații despre lucrarea "Metoda de programare și scheme de ramură în procesele de rezolvare a problemelor de optimizare discrete"