LUCRAREA LABORATORULUI № 4
MĂSURAREA MOMENTELOR DE INERTIA TEL
Obiectiv: Pentru a măsura magnitudinea momentului de inerție al corpului axisimetric (cilindru coaxial) prin vibrația de torsiune, pentru a compara valorile măsurate cu valorile teoretice prezise ale moment de inerție.
Valoarea momentului de inerție a corpului față de o anumită axă (momentul axial de inerție) poate fi calculată din formula
unde este densitatea corpului și R este distanța de la volumul elementar dV la axă. Să calculați cu ajutorul acestei formule magnitudinea momentului de inerție al unui cilindru coaxial de înălțime h. având razele interioare și exterioare ale R1 și R2, respectiv, față de axa sa de simetrie (figura 1).
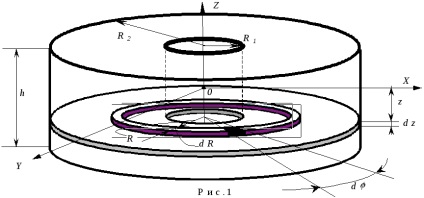
Direcționăm axa Z a sistemului de coordonate de-a lungul axei de simetrie a cilindrului, iar originea sistemului de coordonate (punctul 0) este plasată pe axa în mijlocul înălțimii, adică în centrul de greutate al cilindrului. Împărțim cilindrul coaxial în discuri subțiri de înălțime dz. Pe un astfel de disc, selectăm un strat inelar îngust de rază R și lățime dR. În schimb, selectăm două raze pe acest strat inelar, unghiul dintre ele este o valoare mică d , sectorul inelar. Deoarece dimensiunea acestui sector este foarte mică, nu vom permite o eroare mare dacă volumul lui dV este calculat ca volumul cubului cu laturile Rd , dR și dZ. Astfel, un volum elementar mic poate fi reprezentat în următoarea formă: dV = RdRd dZ
Integrarea pe întregul volum al cilindrului este echivalentă cu integrarea triplu: în intervalul de la 0 la 2 , în Z - în intervalul de la -h / 2 la h / 2. și R în intervalul de la R1 până la R2. Astfel, integrale (1) poate fi scris în următoarea formă:
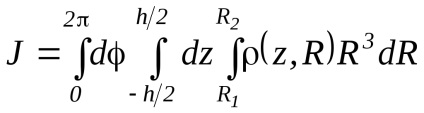
Integrarea cu privire la dă pur și simplu factorul 2 ,
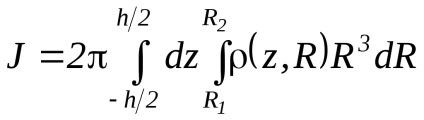
Dacă presupunem că organismul este omogen ( = Const). atunci după integrarea în ceea ce privește z și R. obținem
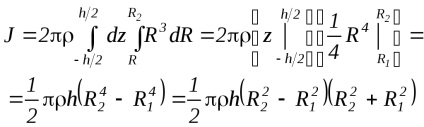
Deci, știind masa cilindrului coaxial, precum și diametrul său intern și extern, îi puteți determina momentul de inerție față de axa simetriei.
Este necesar să se ia în considerare următoarea circumstanță. Formula (2) este aplicabilă pentru a determina magnitudinea momentului de inerție a cilindrului numai dacă este cunoscut în prealabil că cilindrul este omogen. Această ipoteză (despre omogenitate) este absentă în metoda oscilațiilor torsiunii.
2. Calculul integralului din formula (1) este destul de simplu pentru corpurile cu o anumită simetrie. Pentru organele de formă arbitrară, o astfel de integrare nu este posibilă în cazul general. În această situație, pentru a determina momentul inerției, se poate folosi observarea unei mișcări, una dintre caracteristicile acesteia depinzând într-un mod cunoscut în momentul inerției. În această lucrare, o astfel de caracteristică este perioada oscilațiilor torsionale. Metoda oscilațiilor de torsiune face posibilă determinarea valorilor momentelor de inerție pentru corpurile de formă arbitrară care au o distribuție arbitrară a densității în volum.
Vibrațiile torsionale sunt vibrațiile realizate de un corp atașat la o tijă (sau fir), dacă tija (sau firul) este supusă deformării torsiunii. Se știe că atunci când un corp suspendat de un arc supus la deformarea compresiei (tensiunii) face o vibrație, atunci corpul se mișcă transversal în acest caz. Dacă deformările sunt mici, adică Legea lui Hooke este valabilă, atunci perioada acestor oscilații T este determinată de formula
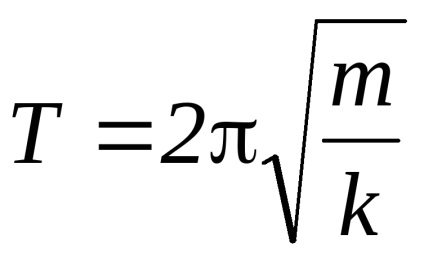
În vibrațiile de torsiune, corpul, așa cum era, efectuează rotații incomplete în raport cu o anumită axă. Prin urmare, formula pentru perioada de oscilație în locul masei include momentul de inerție relativ la axa de rotație și în loc de rigiditatea k, rigiditatea în raport cu deformația de torsiune . Astfel, formula pentru perioada oscilațiilor torsionale ia forma
Relația dintre perioada de oscilație și momentul inerției date de formula (3) ne permite să determinăm în principiu valoarea lui J din măsurătorile perioadei T. dacă se cunoaște valoarea cunoscută. Cu toate acestea, valoarea este de obicei cunoscută cu precizie redusă, prin urmare metoda de măsurare J. bazată pe relația (3) are o eroare sistematică mare.
eroarea de măsurare sistematică datorită erorii , poate fi eliminată dacă metoda vibrațiilor torsionale folosită pentru a determina raportul dintre momentele de inerție ale corpurilor atașate la același fir. Este evident că acest raport nu depinde de valoarea . De fapt, chiar fire atașat la un corp având un moment de inerție în jurul unei axe care coincide cu axa de rotație egală cu J0. Perioada de oscilație T0 a unui astfel de corp este
Dacă un alt corp este atașat la primul corp, al cărui moment de inerție este egal cu J în raport cu axa de rotație, atunci momentul inerției unui astfel de sistem va fi egal cu suma J + J0. În consecință, perioada oscilațiilor unui astfel de sistem se modifică.
Împărțirea (5) de către (4), găsim
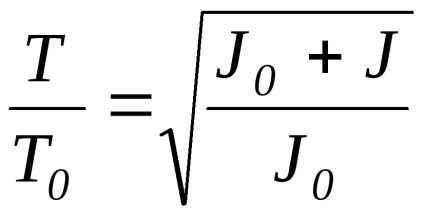
De la Formula (6) arată că prejudecată determinarea J raportul / J0 depinde numai de erorile de măsurare sistematice perioadelor T și T0 oscilațiilor. care au cronometrele moderne sunt mici. Evident că, în cazul în care valoarea J0 este cunoscută în raport cu axa de rotație a oricărui alt considerent, calculând apoi raportul J / J0 cu formula (6), este ușor să se determine momentul J inerție în raport cu aceeași axă de rotație.
Dispozitivul de măsurare a momentului de inerție prin metoda oscilațiilor de torsiune este o coloană colectată pe o bază masivă pentru fixarea probelor de studiu și un milisecunde. Pe coloană cu ajutorul șuruburilor de fixare sunt plasate trei brațe. Parantezele superioare și inferioare au cleme, Angajați pentru fixarea firului de oțel, la care este suspendat cadrul cu platforma sub forma unui disc subțire. Momentul de inerție a cadrului cu platforma J0 față de axa de rotație este cunoscut. Valoarea sa este afișată pe instalație. Designul ramei este astfel încât vă permite să plasați pe platformă diferite corpuri, momentul de inerție care trebuie măsurat. Pe suportul mijlociu este fixată o placă de oțel, care servește drept bază pentru senzorul fotoelectric, electromagnetul și scala unghiulară. Electromagnetul poate schimba poziția de pe placă și poziția sa față de fotosensor este afișată pe scara unghiulară printr-o săgeată atașată la electromagnet.
Panoul frontal al mileazului este:
- cheia "Rețea" este comutatorul principal. Apăsând această tastă, alimentarea cu energie electrică pornește. În același timp, ar trebui afișate două zerouri și becul luminos al fotosensorului trebuie să fie iluminat;
- Tasta "Resetare" - resetați cronometrul. Apăsând această tastă se resetează circuitele blocului de măsurare și se generează un semnal care permite măsurarea;
- tasta "Stop" este sfârșitul măsurătorii. Când această tastă este apăsată, se va genera un semnal pentru a termina numărul de timp;
- tasta "Start" - controlul electromagnetului. Apăsând această tastă se declanșează curentul care alimentează electromagnetul.
Există de asemenea două afișaje digitale pe panoul frontal. Unul arată numărul de perioade de oscilație a cadrului, iar celălalt - timpul în care au loc aceste fluctuații.
Când se apasă tasta "Rețea", cronometrul este setat la starea inițială (zerouri pe indicatoarele digitale) și circuitul de modelare a impulsurilor este blocat. Această blocare este eliminată printr-un semnal care este generat atunci când este apăsată tasta "Resetare". Apăsând tasta "Start" se declanșează electromagnetul, iar oscilațiile de torsiune ale pendulului încep. La momentul primei întreruperi a incidentului fluxului luminos de pe fototranzistor de la bec, se generează un impuls electric care conectează oscilatorul de cuarț la contorul de timp. Contorul numără numărul de impulsuri urmărite de la un oscilator cuarț cu o frecvență de 10 kHz. În același timp, un alt contor numără fiecare (după primul) impuls impar. Trecerea fiecărui astfel de impuls impare corespunde unei singure oscilații, iar indicarea afișării digitale a contorului de perioadă se va schimba cu una.
Când tasta "Stop" este apăsată, se generează un semnal care pregătește circuitele pentru sfârșitul contului. În total, contul se oprește în momentul generării următorului impuls impus de un fotosensor. În același timp, numărul de fluctuații și timpul în care sunt comise sunt afișate pe afișajele digitale. Eroarea sistematică în timpul de măsurare este de 0,02%.
Astfel, metoda de măsurare a momentului axial al inerției unui corp se reduce la următoarele. Mai întâi trebuie să verificăm aplicabilitatea formulei (6), adică asigurați-vă că oscilațiile sunt ușor amortizate. După aceasta, determinați perioada de oscilație a platformei și platformei goale, cu corpul instalat pe ea. Apoi se calculează J din eșantion prin formula (6).
Metoda descrisă este adecvată pentru determinarea momentului de inerție al unui corp de formă arbitrară față de axa oscilațiilor. În cazul particular în care corpul este montat pe o platformă astfel încât axa oscilațiilor să coincidă cu axa de simetrie a corpului, momentul de inerție față de axa de simetrie este determinat de metoda oscilațiilor de torsiune.
PUNEREA ÎN APLICARE A LUCRĂRII ȘI CONDIȚIILE EXPERIMENTALE
1. Porniți dispozitivul apăsând tasta "Rețea", asigurați-vă că indicatoarele glucometrului luminează zerourile și becul bec al fotosensorului este pornit. Instalați electromagnetul într-o anumită poziție și fixați-l cu platforma.
2. Asigurați-vă că oscilațiile pendulului de torsiune sunt puțin amortizate. Pentru a face acest lucru, apăsând succesiv tastele "Resetare" și "Start", determinați numărul de oscilații N, în care amplitudinea scade cu 2-3 ori. Dacă N> 10, atunci atenuarea este mică și este posibilă utilizarea formulei (4). Măsura N pentru o platformă goală și pentru o platformă cu un inel pe ea.
3. Determinați timpul t0. În timpul căruia cadrul cu o platformă goală face N oscilații. Măsurătorile ar trebui efectuate la diferite N (numai 5-7 ori). Evident, T0 = t0 / N. Datele trebuie introduse în tabel. Calculați erorile medii, aleatorii și sistematice.
4. Așezați proba de testare pe platformă. Asigurați-vă că centrul inelului coincide cu centrul platformei. Măsurați perioada de oscilație T. precum și în pasul 3.
5. Calculați momentul inerției inelului cu formula (6).
6. Determinați masa inelului M. Pentru a face acest lucru, se cântărește inelul pe scări tehnice de două ori, așezându-l pe diferite pahare. Găsiți media acestor măsurători, calculați eroarea aleatorie, eroarea sistematică de cântărire fiind considerată egală cu masa celei mai mici greutăți utilizate.
7. Măsurați raza interioară și exterioară a inelului cu ajutorul unui etrier. Măsurați de cel puțin 5 ori. Calculați valoarea medie a lui R1 și R2. erorile lor aleatorii și sistematice.
8. Calculați momentul inerției inelului cu formula (2).
PROCESAREA REZULTATELOR EXPERIMENTALE
Valorile momentelor de inerție ale inelului, măsurate atât prin metoda vibrațiilor prin torsiune, cât și prin metoda cu formula (2), sunt rezultatele măsurărilor indirecte. Obținem formule pentru calculul erorii de măsurare a cantităților J. obținută prin aceste metode. Pentru metoda oscilațiilor de torsiune, în conformitate cu regulile pentru calculul erorii măsurărilor indirecte și a formulei (6), obținem
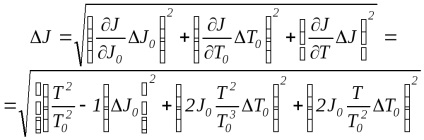
Împărțind ambele laturi ale expresiei rezultate de către J. obținem
Înlocuindu-se în (7) în loc de J0. T0 și T prima aleatoare, apoi erorile sistematice în măsurarea directă, erorile J sunt calculate datorită erorilor aleatoare (oJ) și sistematice (cJ) ale măsurătorilor directe. Eroarea totală este.
Similar, formula este derivată și pentru a calcula eroarea de măsurare printr-o metodă folosind formula (5)
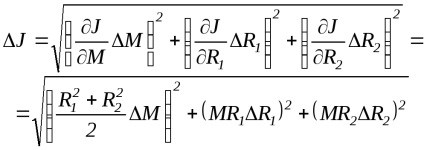
La fel ca înainte, eroarea datorată erorilor aleatorii și sistematice ale măsurărilor directe se calculează folosind formula (8), iar apoi se calculează eroarea totală.
După calcularea erorilor, este posibil să se facă o comparație corectă a rezultatelor măsurării valorilor momentului de inerție obținut prin diferite metode. În cazul în care rezultatele măsurătorilor diferă cu mai mult decât erorile experimentale, este necesar să se concluzioneze că pot exista motive pentru această discrepanță.