Extinderea seriei triungometrice Fourier cu ajutorul lui Wolfram Alpha
În practică, în special pentru studenți și pentru aplicații tehnice, de multe ori este nevoie pentru a găsi rapid extinderea acesteia sub forma de serii Fourier trigonometrice. Prin urmare, unii cititori întreba: cum să obțineți Wolfram Alpha pentru a aduce extinderea unei funcții date într-o serie Fourier în partea de sus a paginii, direct sub câmpul din dreapta al cererii.
Răspunsul la acest lucru am găsit logic.
Deoarece forma trigonometrică a unei serii Fourier sistem Alpha Wolfram consideră subsidiar, acest lucru înseamnă că, la început calculează coeficienții de serie exponențială, și numai apoi le convertește (simplifică conduce la forma trigonometrice), folosind formula lui Euler (formula lui Euler).
Desigur, pentru a obține prima extindere a funcției în serie Fourier trigonometrice, aveți nevoie pentru a pune imediat sistemul tocmai această sarcină, și anume de a simplifica extinderea funcției într-o serie Fourier, care este ușor de făcut utilizând cuvântul cheie simplifica.
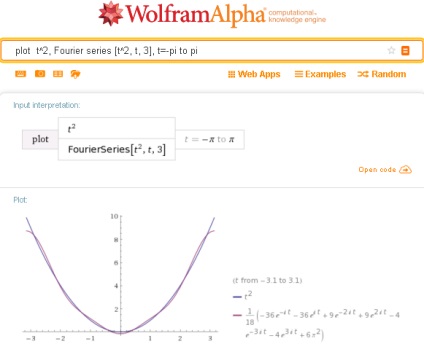
Astfel, pentru a obține extinderea unei funcții într-o serie Fourier trigonometrică cu ajutorul lui Wolfram Alpha, ar trebui să utilizați o interogare a formularului:
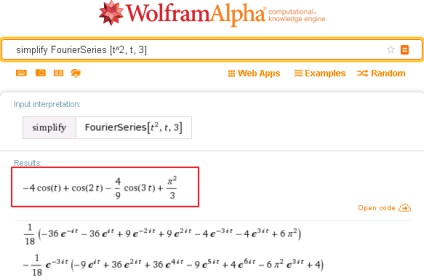
După cum se vede în figură, aici, sistemul emite primul primele 3 termenii funcției de expansiune t ^ 2 în serie Fourier trigonometrică și au arată seria Fourier secundar corespunzătoare în formă exponențială.
Apropo, dacă brusc interesat de cât de bine seria Fourier aproximează această funcție, se poate observa destul de ușor. Este suficient pentru a compara cele două grafice în același sistem de coordonate - graficul funcției și apropierea acesteia la trigonometrice specificându-le separate prin virgulă: