Luați în considerare semnele de catastrofe. Existența unei catastrofe este evidențiată de puncte critice speciale ale unei familii de funcții potențiale care descriu un sistem sau un fenomen. Cu toate acestea, astfel de puncte nu pot fi recunoscute imediat.
De exemplu, o funcție potențială este foarte complexă sau nu este exact cunoscută. Chiar mai rău, atunci când sistemul nu este gradientului și foarte rău atunci când nu există nici măcar o vagă idee despre forma ecuației, care să asigure în mod adecvat, care descrie sistemul.
Cu toate acestea, catastrofele apar adesea în situații reale și, prin urmare, este important să le recunoaștem în timp. Catastrofele au trăsături distinctive - semne care atrag atenția asupra acestui proces.
Imediat ce una dintre ele este fixată, adică se stabilește un semn care indică prezența unei catastrofe în sistem, parametrii de control ai sistemului pot fi modificați astfel încât să găsească semnele rămase, care trebuie să se dovedească în mod necesar să se afle în condițiile corespunzătoare. Stabilirea prezenței și a tipului de dezastru în caz de incertitudine în descrierea sistemului ajută la determinarea:
- o funcție simplificată a potențialului model care depinde numai de variabilele de stare semnificative și de parametrii de control;
- o parte structurală stabilă a unei funcții potențiale care poate spune ce fel de proces are loc efectiv;
- Tipul ecuației pentru sistem și modul în care se introduce funcția potențială;
- utilizarea inutilă a ecuațiilor în general.
Descrierea semnelor de dezastre
modalitate
Sistemul poate avea două sau mai multe stări diferite în anumite zone ale modificării parametrilor de control. De exemplu, dacă parametrii de control ai sistemului sunt în zona umbrită, sistemul poate fi în trei stări diferite (de exemplu, accidentul de asamblare din Figura 1).
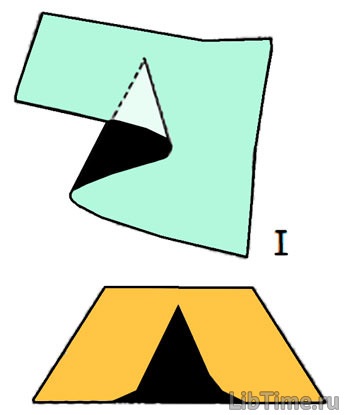
Figura 1 - Modalitatea și indisponibilitatea într-un ansamblu de catastrofe
inaccesibilitate
Există o zonă de stări instabile de echilibru instabil, care nu pot fi atinse prin mișcarea de-a lungul oricăror stări stabile. În Fig. 1 stratul de mijloc este inaccesibil.
Curse catastrofale
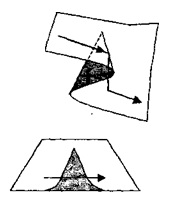
Figura 2 - Curse cataclismice
mici modificări în valorile parametrilor de control pot provoca schimbări mari în valorile variabilelor de stare ca modul în care sistemul sistemul de sare de la un minim local la altul, trecerea de la un cartier de un minim local la altul este o schimbare mare în valorile schimbării stării care are loc la scară ultra-rapid .
În Fig. 2 saltul are loc imediat ce starea sistemului trece de la un strat al suprafeței de catastrofă a ansamblului la celălalt.
diferență
Modificările finale ale valorii parametrilor de control conduc la modificări finale ale valorilor variabilelor de stare la punctul de echilibru.
De obicei modificările mici ale valorilor inițiale ale parametrilor de control conduc doar la o ușoară modificare a valorilor inițiale și finale ale variabilelor de stare. Cu toate acestea, în prezența unei catastrofe, mici modificări ale valorilor inițiale ale variabilelor de stare pot duce la schimbări mari în valorile finale ale acestor variabile.
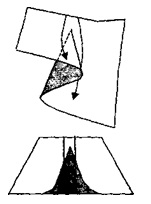
Figura 3 - Diferența
În Fig. 3 se arată că traiectoriile modificării parametrilor de control pentru stările inițiale apropiate ale sistemului conduc la o diferență semnificativă între stările finale ale sistemului.
Histerezis și ireversibilitate
Histerezisul are loc atunci când procesul nu este complet reversibil. Sari de la un minim local de 1 la un minim local de 2 nu poate avea loc în aceleași valori ale variabilelor de control, cu toate că saltul de la punctul 2 la punctul 1 a avut loc în timpul mișcării în direcția opusă.
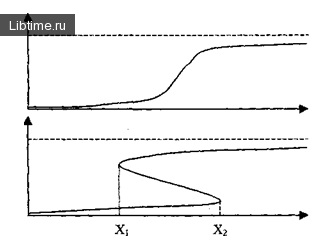
Figura 4 - Fenomenul histerezis
Să luăm în considerare dependența de eficiența muncii și de remunerare. pentru care lucrează. Odată cu creșterea remunerației, creșterea eficienței muncii va crește. Dacă recompensa nu este suficientă, angajatul este foarte încercat. Pe de altă parte, toată lumea are o limită de eficiență și, indiferent de modul în care se ridică recompensa, nu va fi posibil să se obțină un efect mai mare.
Această situație poate fi descrisă aproximativ prin funcția prezentată în Fig. 4.
Luați în considerare acum un proces dinamic în care plata poate crește și scădea. Dacă plata inițială este scăzută, atunci eficiența muncii este de asemenea scăzută. Odată cu creșterea plății, eficiența crește, dar încet, deoarece, potrivit angajatului, creșterea plății este insuficientă pentru a spori eficiența muncii.
Acest lucru se va întâmpla până în momentul X2, când o creștere ulterioară a plății necesită o tranziție la un nivel calitativ nou de performanță. Există o schimbare bruscă a eficienței.
Dacă, dimpotrivă, în momentul inițial, plata este ridicată, atunci eficiența este menținută la un nivel ridicat. În reducerea plății se înregistrează o ușoară scădere treptată a eficienței (se produce o anumită inerție, conform căreia o persoană continuă să lucreze în modul obișnuit).
Acest lucru se întâmplă până când plata ajunge la un nivel destul de scăzut al lui X1. În acest moment, există o scădere accentuată a eficienței, deoarece nu există niciun stimulent pentru a-și menține nivelul ridicat. Figura arătată în Fig. 4b, se numește buclă de histerezis.
Strict vorbind, aceasta nu este o funcție, deoarece aceeași valoare X poate corespunde cu două (sau chiar trei) W. Valoarea Prezența unei multitudini de astfel de X - [X2 Xp] și conduce la posibilitatea unor schimbări catastrofale în starea sistemului. Setul [Xt; X2] se numește set de bifurcație. și anume astfel, pentru valorile parametrilor din care sunt posibile mai multe stări diferite ale sistemului. În Fig. 5 prezintă același fenomen într-un sistem tridimensional.
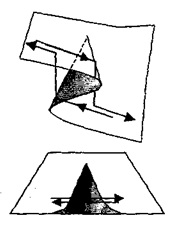
Figura 5 - ireversibilitatea într-un sistem tridimensional
Deci, o catastrofă este o schimbare bruscă și bruscă a stării sistemului, cu o schimbare lentă a parametrilor (sau a variabilelor de control).
Revenind la exemplul, veți observa că atunci când rotiți axa și ia în considerare plata în funcție de eficiență, avem de-a face cu un polinom de gradul trei (Fig. 4). Acest polinom nu are nici o extrema, iar in Fig. 4b are două extreme. Evident, numărul de puncte extreme depinde de coeficienții polinomului, adică parametrii sistemului.
Să luăm în considerare natura locală a posibilelor funcții. Proprietățile stărilor de echilibru depind de tipul și proprietățile funcției potențiale, care descrie comportamentul sistemului. Anterior, sa considerat clasificarea stărilor de echilibru în sistemele bidimensionale, în care au fost posibile opt variante de echilibru diferite. Dacă variabilele de stare ale sistemului sunt mai mari, atunci clasificarea completă a stărilor de echilibru se dovedește a fi foarte dificilă.
Teoria catastrofelor face posibilă realizarea unei astfel de clasificări pentru o clasă destul de largă de sisteme neliniare.
Să analizăm ce transformări sunt posibile pentru posibilele funcții într-o vecinătate a stării de echilibru. Aceste transformări fac posibilă simplificarea funcției și aducerea acesteia într-o formă simplă locală și evidențierea catastrofelor.
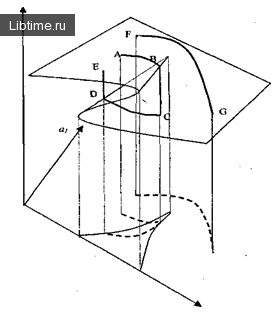
Figura 6 - Accidentul asamblării
După cum se vede din figură, sistemul începe mișcarea sa de la punctul A, atâta timp cât posibil, să se deplaseze pe partea de sus a suprafeței, până când ajunge la singularitatea stabilit la punctul B. Apoi, sistemul efectuează un salt ascuțit în jos la punctul C și se duce la partea de jos a suprafeței.
Dacă sistemul își pornește mișcarea pe fund, va traversa bifurcația setată la punctul D și va face un salt ascuțit la partea superioară a suprafeței. Un alt comportament al sistemului este posibil, care nu include tranziții ascuțite. De exemplu, de-a lungul căii FG, dacă unul dintre parametrii sistemului se poate modifica rapid.
Aplicațiile economice ale teoriei catastrofelor se bazează în mare parte pe aspecte geometrice, în special pentru descrierea comportamentului economic se aplică tocmai catastrofa asamblării. Alte dezastre elementare sunt greu de ilustrat, deoarece necesită consolidarea unuia sau mai multor parametri.
Teoria catastrofelor este folosită pentru a studia multe probleme, inclusiv colapsul burselor, comportamentul guvernamental, macromodelele, aspectele structurale ale presupunerii lui Walras etc.