Orice sistem de control. lucrul cu semnale digitale, poate fi reprezentat sub forma fig. 2.44 (a) în cazul în care stările semnalelor de ieșire Z, Y, X, W, și așa mai departe. E. Determinată de valorile intrărilor A, B, C, D, și așa mai departe. D. Munca poate organiza sistemul de management folosind o combinație a două metode de bază.
Cea mai simplă dintre aceste metode este logica combinatorică. Când sistemul poate fi împărțit în blocuri mai mici, ca în Fig. 2.44 (b), cu o ieșire pentru fiecare bloc, starea de ieșire fiind determinată numai de valorile intrărilor corespunzătoare. De exemplu, supapa de încărcare a pompei hidraulice va fi activată dacă:
Pompa este pornită ȘI
(Modul "UP" este selectat ȘI comutatorul de limitare de vârf nu sa declanșat) SAU
(Este selectat modul "Jos" și comutatorul de limită inferior nu funcționează)
Lucrarea acestei supape de încărcare poate fi organizată folosind un program simplu sub forma unui circuit multi-etapă sau a unei structuri logice, ca în Fig. 2,45, dar este de preferat să se dezvolte un mod standard de creare a unui program bazat pe logica combinatorică.
Prima etapă este divizarea sistemului de control într-o serie de blocuri mici, fiecare dintre ele având o ieșire și mai multe intrări. În plus, pentru fiecare ieșire este necesară compilarea unei așa-numite tabele de adevăr, în care trebuie să fie scrise toate stările posibile de intrare și stările lor de ieșire corespunzătoare. În Fig. 2.46 (a) avem ieșire Z, în funcție de cele patru intrări A, B, C, D. Totalul există 16 combinații posibile de condiții de intrare, un Z este activat (de ex. E. Este adevărat), doar patru dintre ele. Aceasta poate fi afișată imediat ca un circuit cu mai multe trepte în Fig. 2.46 (b) sau logica din Fig. 2.46 (c), unde fiecare legătură sau poarta AND corespunde unei linii a tabelului de adevăr.
Utilizarea tabelelor de adevăr pentru sinteza schemelor logice combinatoriale conduce direct la o structură constând din elemente AND / OR și în limba tehnică numită "suma produselor".
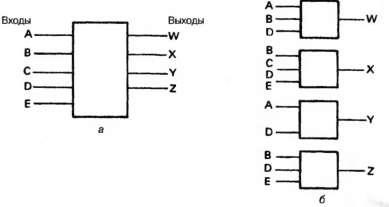
Fig. 2.44. Logica combinatorică: (a) reprezentare la nivel înalt; (b) subdiviziunea în blocuri mai mici
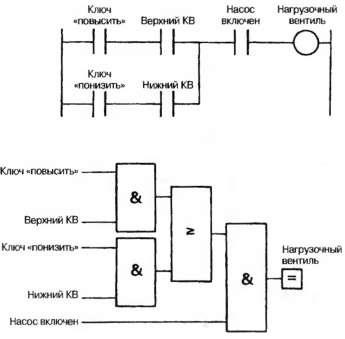
Fig. 2.45. Logica combinatorică într-o schemă în mai multe etape și în notație logică
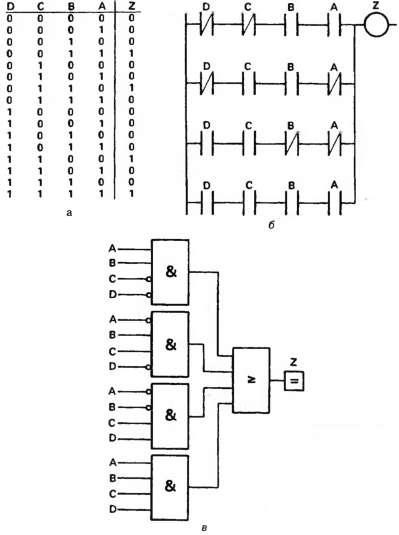
Fig. 2,46. Logica combinatorică ca o consecință a tabelului adevărului: (a) tabelul de adevăr; (b) punerea în aplicare a tabelului de adevăr; (c) punerea în aplicare ca o schemă logică
O întrebare firească apare: „Este o astfel de structură simplă?“ Răspunsul este nu, pentru că există metode, cum ar fi hărți Karnaugh și algebra boolean, oferind o soluție mai simplă. Dacă structura este creată din porți logice sau relee, este de dorit să se facă cu un număr minim de porți sau contacte pentru a reduce costurile de proiectare. La scrierea unui program pentru PLC, nu sunt necesare contacte suplimentare, astfel încât obiectivul principal ar trebui să fie transparența programului și nu simplitatea acestuia. Una dintre simplificărilor este întotdeauna recomandat să facă (din nou, pentru transparență), este de a exprima link-urile generale de contact, așa cum este prezentat în Fig. 2.47.
De exemplu, luați în considerare panoul de control al unității de pompare, prezentat în Fig. 2,48 (a). Din motive de ieftinitate, comutatorul cu trei poziții este conectat direct la două grupuri de contacte, așa cum se arată în Fig. 2.48 (b) (în practică, acest lucru nu se face
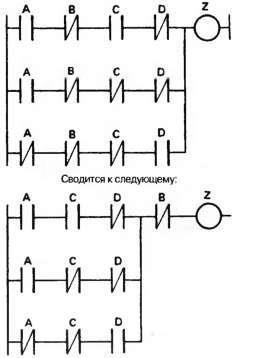
Fig. 2.47. Simplificarea logicii combinatoriale
Se recomandă ca, în cazul unei întreruperi a alimentării, ambele pompe să fie pornite). Tabelul de adevăr pentru acest caz duce la schema în mai multe etape din Fig. 2.48 (c), dar schema de complexitate minimă are forma Fig. 2,48 (d). Acesta din urmă, totuși, nu reflectă funcționarea comutatorului și, prin urmare, complică oarecum detectarea defecțiunilor.
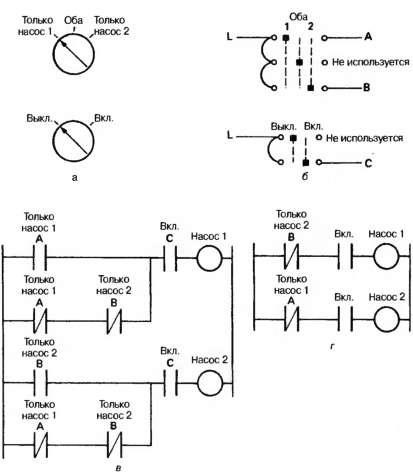
Fig. 2,48. Minimizarea nu promovează transparența: (a) panoul de control; (b) conectarea telecomenzii; (c) un program bazat pe un tabel de adevăr; (d) un program de complexitate minimă