1. Care este momentul forței în raport cu punctul situat pe linia de forță?
Care este umărul forței relativ la un punct localizat arbitrar?
Dimensiunea și direcțiile vectorului principal depind de poziția centrului turnării?
Indicați toate cazurile posibile de aducere la punct a unui sistem planar de forțe inferioare.
În acest caz, vectorul principal coincide cu rezultatul?
În ce cazuri un sistem plat de forțe poate fi echilibrat de o forță? Cum este linia acțiunii sale?
La ce valoare a vectorului principal și momentul principal este sistemul de forțe în echilibru?
Lucrarea de laborator № 4 Schemele de calcul ale grinzilor și determinarea reacțiilor suporturilor lor
Bucăți de lucru - să se familiarizeze cu dispozitivul suporturilor de grinzi, să calculeze schemele de proiectare ale grinzilor și să determine reacțiile suporturilor lor.
O justificare teoretică. Un corp solid este considerat a fi un fascicul, în care lungimea este mult mai mare decât dimensiunile transversale; setul (locul geometric) al centrelor de greutate ale tuturor secțiunilor transversale se numește axa barei. Un fascicul cu o axă dreaptă, plasat pe suporturi și îndoit de încărcăturile aplicate, este numit un fascicul. Grinzile se găsesc în multe mașini și structuri și servesc la perceperea forțelor orientate perpendicular pe axa lor longitudinală.
Grinzile au dispozitive speciale de susținere pentru a le interfața cu alte elemente structurale și a le transfera forțe. Suporturile fasciculului pot fi împărțite în următoarele trei tipuri:
Suportul mobil (suport pe role) (fig.1, a).
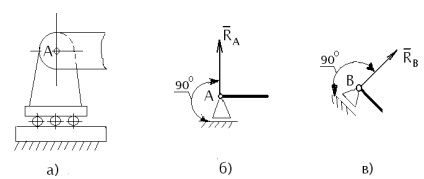
Racordarea tijei la suportul mobil permite rotirea tijei în jurul axei balamalei și deplasarea liniară paralelă cu planul de susținere. Aici știm punctul de aplicare al reacției de sprijin
Trebuie avut în vedere faptul că suprafața de susținere a suportului mobil nu poate fi paralelă cu axa fasciculului (fig.1, c). Reacția suportului în acest caz nu formează un unghi drept cu axa fasciculului.
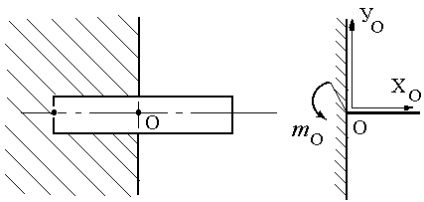
Suport fix cu fixare (figura 2, a).
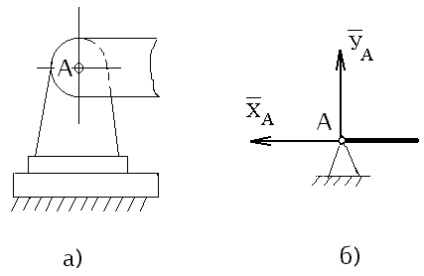
Racordarea tijei la suportul fix permite doar rotirea tijei în jurul axei balamalei. În acest caz, numai punctul de aplicare al reacției de susținere este cunoscut - centrul balamalei, direcția reacției nu este cunoscută, deoarece depinde de sarcina aplicată pe grindă. Prin urmare, în loc de reacția completă a suportului fix, două componente reciproc perpendiculare
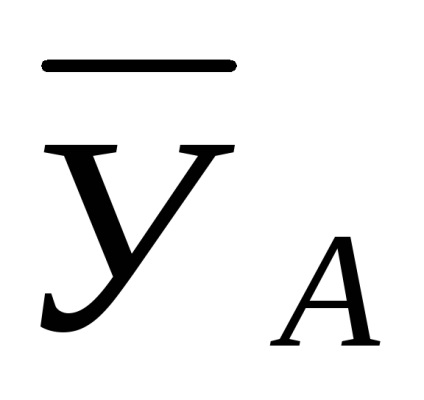
Reprezentarea schematică a suportului fix pivotat este prezentată în Fig.2, b conform ESKD GOST 2.770-68.
Etanșarea rigidă (prinderea) (fig.3, a) nu permite deplasarea liniară sau rotirea secțiunilor transversale ale fasciculului fix.
Nu numai direcția reacțiilor, ci și punctele de aplicare a acestora, nu sunt cunoscute pentru etanșarea tare, prin urmare, pentru a determina reacția de referință, este necesar să se găsească două componente reciproc perpendiculare
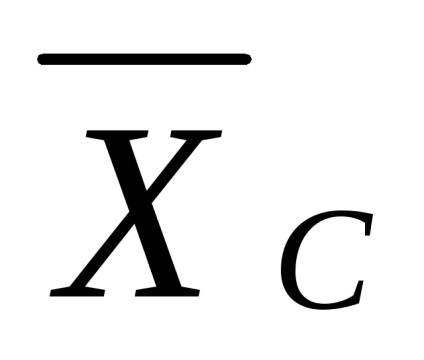
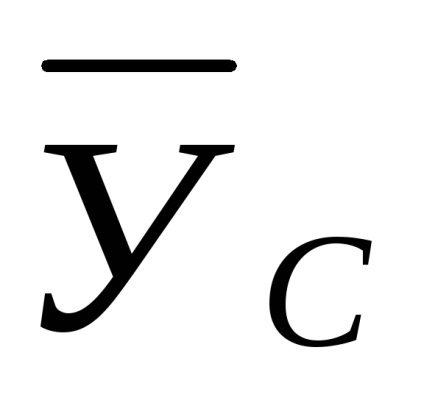
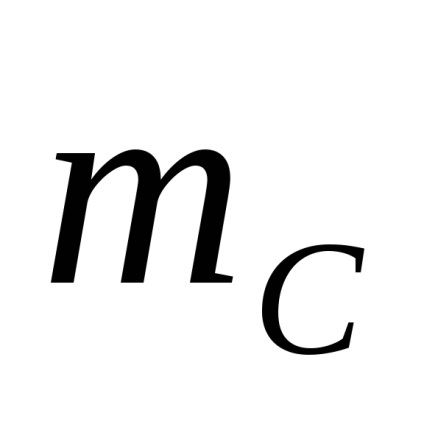
Figura 3b prezintă o reprezentare schematică a unei etanșări rigide.
Echilibrul fasciculului sub acțiunea oricărui sistem de forțe externe situate în același plan poate fi asigurat de o îmbinare rigidă sau de două suporturi: mobilă și fixă.
Figura 4 prezintă un fascicul încărcat cu forțe concentrate
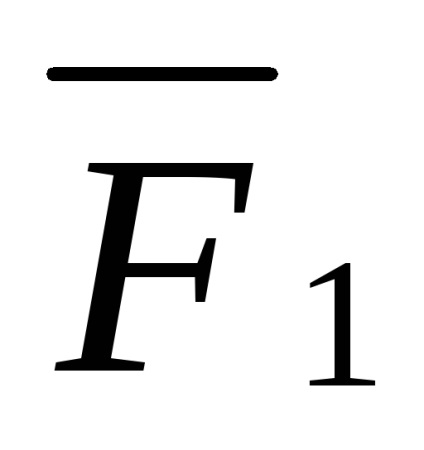
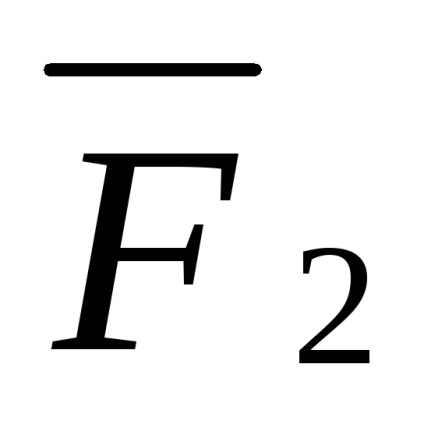

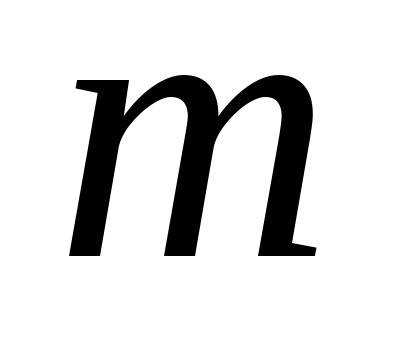
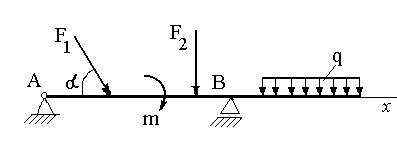
Răspunsurile suportului fasciculului sunt determinate prin intermediul a trei ecuații de echilibru:
Forma ecuațiilor de echilibru prezentată aici este dispariția sumelor momentelor cu privire la două puncte A și B - centrele balamalelor suportului grinzilor și dispariția sumei proiecției pe axa x. Axa x coincide cu axa fasciculului.
Pentru determinarea reacției de fixare rigidă a suportului, se recomandă aplicarea următoarei trei ecuații de echilibru:
și anume proiecția tuturor forțelor pe axele x și y dispare și suma momentelor tuturor forțelor relative la punctul C dispare.