Acasă | Despre noi | feedback-ul
1. Proiecții centrale și proprietățile lor de bază.
Atunci când proiecția centrală (construcția proeminențelor centrale) este dată planului proeminențelor și centrului proeminențelor - un punct care nu se află în planul proeminențelor. În figura 1.1, planul P este planul proiecțiilor, punctul S este centrul proiecțiilor.
Pentru a proiecta un punct arbitrar prin acesta și centrul proiecțiilor, trageți o linie dreaptă. Punctul de intersecție al acestei linii cu planul proiecțiilor este proiecția centrală a punctului dat pe planul ales de proiecții.
În figura 1.1, proiecția centrală a punctului A este punctul a de intersecție a liniei SA cu planul P. Proiecțiile centrale bp, cp, punctele dp B, C, D pe planul P sunt, de asemenea, construite.
Liniile drepte care trec prin centrul proiecțiilor și punctelor proiectate sunt numite linii de proiectare.
Proiecțiile centrale bp și cp ale două puncte diferite B și C în spațiu, care sunt situate pe o singură linie proeminentă, coincid. Tot setul de puncte de spațiu aparținând unei linii de proiectare are, la un centru de proiecție, o proiecție centrală pe un anumit plan de proiecție.
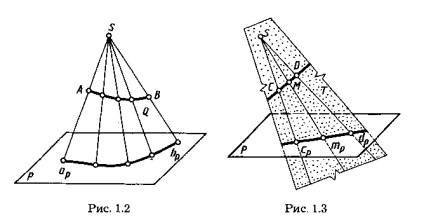
Pentru a asigura reversibilitatea desenului, adică pentru a determina în mod unic poziția unui punct din spațiu de la proiecție, sunt necesare condiții suplimentare, de exemplu, puteți specifica un al doilea centru de proiecții. Prin proiecția centrală, proiecția oricărei linii sau a unei suprafețe poate fi construită ca setul de proiecții ale tuturor punctelor sale (vezi figurile 1.2, 1.3). În aceste linii proeminente (în întregime) efectuate prin toate punctele unei linii curbe formează o suprafață conică proiectată (fig. 1.2), sau poate fi în același plan (vezi. Fig. 1.3), care se numește proiecție.
Proiecția curbei liniei este linia de intersecție a suprafeței conice proeminente cu planul proeminențelor. Astfel, în figura 1.2 poverhnostQ conică proeminentă se intersectează cu planul P al curbei proiecțiilor apbp care linia de proiecție linii de proiecție AV.Odnako nu identifică linia proiectată, deoarece suprafața proeminentă poate fi un număr infinit de linii proeminente în aceeași linie în planul proiecții (figura 1.4).
Atunci când se proiectează o linie dreaptă care nu trece prin centrul proeminențelor, suprafața proeminentă este planul. Astfel, în Figura 1.3 planul proeminent T format prin liniile SC și SD proiectat, care trece prin punctele C și D o linie dreaptă, intersectează planul P al proiecțiilor privind cpdp înainte, care este proiecția liniei CD. Corespunzător, proiecția punctului M al CD-ului direct aparține proiecției cpdp.
Pentru a construi proiecții de linii, suprafețe sau corpuri, este adesea suficient să se construiască proiecții ale unor anumite puncte caracteristice. De exemplu, atunci când construim proiecțiile Proiectării triunghiului ABC (Figura 1.5) pe planul de proiecție, este suficient să construim proiecțiile ap, bp, cp ale celor trei puncte - vârfurile A, B, C.
Proprietățile proiecției centrale.
1. Cu proiecție centrală:
a) punctul este proiectat într-un punct;
b) o linie dreaptă care nu trece prin centrul proiecțiilor este proiectată într-o linie dreaptă (proiectând o linie dreaptă - până la un punct);
c) o bidimensional) model plat (care nu aparțin planului proeminent este proiectat sub forma bidimensionale forme (forme aparținând planului proeminent proiectat împreună cu ea sub forma unei linii drepte);
d) figura tridimensională este afișată într-o formă bidimensională.
2. Proiecțiile centrale ale figurilor își păstrează apartenența reciprocă, continuitatea și alte proprietăți geometrice.
3. Pentru un anumit centru de proiecție de proiecție, cifrele de pe planurile paralele sunt similare.
4. Proiecția centrală stabilește o corespondență unu-la-unu între figură și imaginea ei, de exemplu imaginile de pe un ecran de film, film.
Proiecțiile centrale sunt folosite pentru a descrie obiectele în perspectivă. Imaginile din proiecțiile centrale sunt clare, dar pentru desenul tehnic sunt incomod, deoarece nu se observă măsura.
2. Proiecții paralele și proprietățile lor de bază.
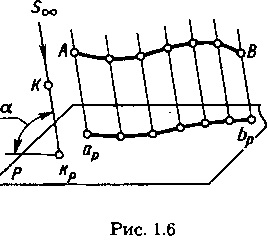
Proiecția paralelă (Figura 1.6) poate fi considerată un caz special de proiecție centrală, în care centrul proiecțiilor este îndepărtat până la infinit (Soo). Pentru proiecția paralelă se utilizează linii de proiectare paralele, desenate într-o anumită direcție în raport cu planul proeminențelor. Dacă direcția de proiecție planul de proiecție perpendiculară, numită proiecție dreptunghiulară sau ortogonale, în alte oblică sluchayah- (Fig. 1.6 direcția de proiecție este indicată printr-o săgeată la un unghi nu este egal cu 90 ° față de planul P al proiecțiilor).
În cazul proiecției paralele, toate proprietățile proiecției centrale sunt reținute și apar următoarele proprietăți noi.
1. Proiecțiile paralele ale liniilor paralele sunt paralele, iar raportul dintre lungimile segmentelor acestor linii este egal cu raportul dintre lungimile proiecțiilor lor.
Dacă liniile MN și KL (figura 1.7) sunt paralele, atunci planurile Q și T proeminente sunt paralele, deoarece liniile intersectate în aceste planuri sunt reciproc paralele: MN || Prin ipoteză, Aar || Csp || S. Prin urmare, proiecțiile mp np și kp lp sunt paralele ca liniile de intersecție a planurilor paralele Q și T cu planul P.
Se marchează un segment arbitrar AB pe linia MN și un segment segmental arbitrar pe linia KL. Tragem în planul Q prin A linia A-1 || iar în planul T prin punctul C linia dreaptă
C-2 || cpdp. Segmentele [A-1] = [apbp], [C-2] = [Cpdp] ca segmente paralele între paralele. Segmentele C-2 || c, dP || appp și, în consecință, C-2 || A- 1. Segmentele B-1 || D-2 || S, triunghi AB-1
triunghi CD-2, deoarece toate laturile lor sunt reciproc paralele. Din similitudinea triunghiurilor AB-1 și CD-2 rezultă:
Din cele considerate, rezultă:
a) dacă lungimea unui segment de linie este împărțită printr-un punct într-un anumit punct, atunci lungimea proiecției segmentului este împărțită prin proiecția acestui punct în același raport (Figura 1.8):
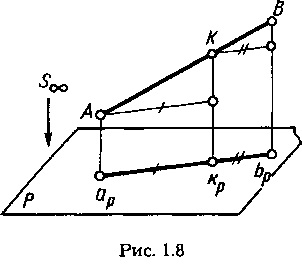
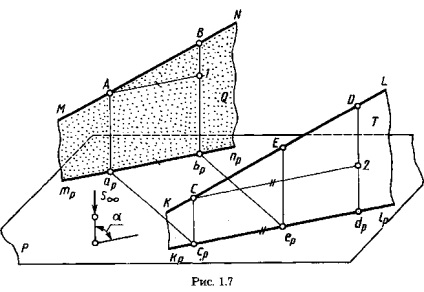
b) proiecțiile cu lungimi egale de linii paralele sunt reciproc paralele și egale în lungime.
Acest lucru este evident, din moment ce ((a se vedea figura 1.7) pentru | AB |: | CD | = 1 va fi | apbp | = | cp dp |. Prin urmare, cu o proiecție oblică în cazul general, o paralelogramă, un romb, un dreptunghi, un pătrat sunt proiectate într-o paralelogramă.
2. O figura plană paralelă cu planul proiecțiilor este proiectată prin proiecție paralelă pe acest plan în aceeași figură.
3. Transferul paralel al unei figuri în spațiul sau în planul proiecțiilor nu modifică forma și dimensiunea proiecției figurii.
Proiecțiile paralele, la fel de centrale la același centru de proiecție, nu asigură reversibilitatea desenului. Folosind tehnici de proiecție paralelă a unui punct și a unei linii, este posibil să se construiască proiecții paralele ale unei suprafețe și ale unui corp. Proiecțiile paralele sunt folosite pentru a construi imagini vizuale ale diferitelor dispozitive tehnice și detaliile acestora, de exemplu proiecții axonometrice, discutate mai jos.
2. Proiecție dreptunghiulară (ortogonală).
Un caz particular de proiecție paralelă, în care direcția de proiecție este perpendiculară pe planul de proiecție, se numește proiecție dreptunghiulară sau ortogonală. O proiecție dreptunghiulară (ortogonală) a unui punct este baza unui perpendicular tras dintr-un punct în planul proiecțiilor. Proiecția dreptunghiulară dp a punctului D este prezentată în figura 1.9.
Pe lângă proprietățile proiecțiilor paralele (oblice), proiecția ortogonală are următoarea proprietate:
proiecțiile ortogonale ale două linii drepte reciproc perpendiculare, una dintre ele fiind paralelă cu planul proeminențelor, iar cealaltă nu este perpendiculară pe aceasta, sunt reciproc perpendiculare.
Să dovedim asta. În figura 1.10, unghiul ABC = 90 °; (AB) || P; (CB) nu este perpendiculară pe P. Vom dovedi că unghiul arbp = 90 °.
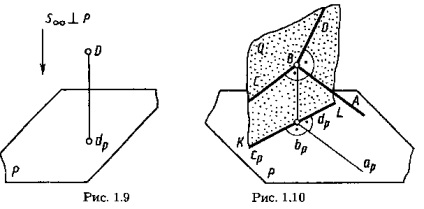
Corespunzător, pentru un unghi DBA = 90 °, (DB) nu este perpendicular pe P și (AB) || P avem:
Proiecția ortografică are mai multe avantaje față de proiecția paralelă centrală și oblică. Pentru ei, în primul rând, simplitatea construcțiilor geometrice ale proiecțiilor ortogonale ale punctelor și conservarea sub proiecții în anumite condiții ale formei și dimensiunile unei preocupări proiectate.
Aceste avantaje au oferit utilizarea proiecției ortogonale pentru dezvoltarea desenelor în toate sectoarele industriale și în construcții.
3. Proiecția în trei planuri de proiecții reciproc perpendiculare.
Reversibilitatea desenului poate fi asigurată prin proiectarea în două planuri non-paralele ale proiecțiilor.
Pentru confortul proiecției sunt alese două planuri reciproc perpendiculare ca cele două planuri de proiecție (Figura 1.11). Unul dintre ele este plasat, de obicei, pe orizontală - se numește planul orizontal al proiecțiilor, celălalt - pe verticală. Planul vertical este numit planul frontal al proiecțiilor. Aceste planuri de proiecții se intersectează de-a lungul unei linii numită axă de proiecție.
Axa de proiecție împarte fiecare dintre planurile de proiecție în două jumătăți de plan.
Denumiți planul de proiecție cu litere: V - frontal, H - ax orizontal de proiecție - cu litera x sau în forma
fracțiuni V / H. Planele V și V H formează sistemul, N. (Pe lângă aceste denumiri plane de proiecție utilizate în literatură și alte denumiri de exemplu litere π cu indici).
Planurile proeminențelor, care se intersectează, formează patru unghiuri dihedral, dintre care cel prezentat în figura 1.11 (cu notația fețelor V, H) este considerat primul.
In desenele multe detalii industria funcționează, de asemenea, într-un sistem de două planuri reciproc perpendiculare care se intersectează pe axa verticală z a proeminențelor (fig. 1.12). In acest plan de proiecție frontală este lăsat ca planul V, și la acesta perpendicular și notat cu numitul profil W proiecție plan.
Într-un sistem de două planuri de proiecții reciproc perpendiculare, proiecția orizontală a unui punct este proiecția dreptunghiulară a unui punct pe planul orizontal al proeminențelor;
Proiecția frontală a unui punct este proiecția dreptunghiulară a unui punct pe planul frontal al proeminențelor.
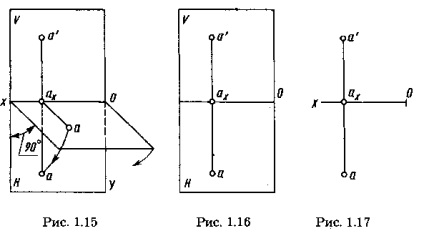
O reprezentare vizuală a construcției proiecțiilor unui punct arbitrar A în sistemul V, H este prezentată în Figura 1.13. Proiecția orizontală indicată de a este găsită ca intersecția perpendicularului trasată de la punctul A la planul H cu acest plan. Proiecția frontală, desemnată cu un ", se găsește ca intersecția perpendicularului tras de la punctul A la planul V, cu acest plan.
Liniile proeminente Aa 'și Aa, perpendiculare pe planurile V și H, aparțin planului Q. Este perpendiculară pe planurile proeminențelor și intersectează axa proiecțiilor la axa punctului. Trei planuri Q, V și H mutuale perpendiculare se intersectează de-a lungul liniilor perpendiculare, adică liniile directe aaax. aax și axa x sunt reciproc perpendiculare.
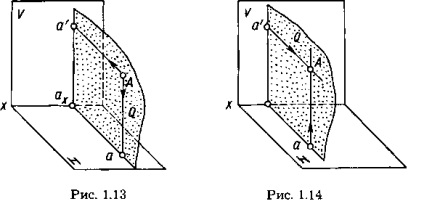
Astfel, două proiecții dreptunghiulare ale unui punct determină complet poziția sa în spațiu față de un sistem dat de planuri de proiecție reciproc perpendiculare.
În cele ce urmează, proiecțiile dreptunghiulare ale unui punct într-un sistem de planuri de proiecții reciproc perpendiculare vor fi numite proiecții ortogonale ale unui punct.