Cantitatea QV (z) corespunde schimbării potențialului energetic al sarcinii pozitive în valorile SCR ale energiei relative în vrac semiconductoare (la z, tinde la infinit).
Distribuția taxei induse într-o grosime a stratului înseamnă că potențialul în semiconductor lin atenuat de o anumită valoare la suprafață la o valoare nulă în afara IPF. Amplitudinea încărcării spațiului distribuit (Z) și potențialul câmpului electrostatic din el V (z) sunt în corespondență unu-la-unu cu celălalt prin ecuația Poisson
unde # 949; 0 - constanta dielectrică a vidului;
Este constanta dielectrică a semiconductorului.
Toate nivelurile de energie care existau în semiconductor la un anumit punct z în absența încărcării induse sunt deplasate de valoarea qV (z) a SCR.
Dacă exprimă schimbarea în potențiale unități T K0 de energie și de a introduce notația Y (z) = QV (z) / (K0 T), ecuația Poisson ia forma
După cum se știe bine, pentru anumite condiții limită, soluția acestei ecuații este o anumită funcție Y (z), care se descompune adânc în semiconductor. Mărimea acestei funcții schimbă toate nivelurile de energie fără dimensiuni (în k0 T) relative la valorile sale fără dimensiuni înainte de apariția HMO. Aceeași cantitate determină îndoirea fără dimensiuni a benzilor de energie în fiecare punct z.
Cantitatea Y (z) se numește potențial electrostatic de suprafață fără dimensiuni.
Distanța de la mijlocul benzii interzise la nivelul Fermi este marcată cu litera # 981; iar valoarea sa pe suprafață este # 981; s. Spre deosebire de potențialul electrostatic fără dimensiuni # 981; s se numește potențialul de suprafață. În general, în literatura științifică despre semiconductori, indicele s înseamnă cantitatea legată de suprafață, deoarece s este prima literă a cuvântului englez "surface".
În conformitate cu o capacitate de amortizare lină variază ușor la toate poziție nivelurile relativ la nivelul Fermi, care este cunoscut, este o măsură a energiei medii a purtătorilor de sarcină pe tot cristalul și deci rămâne neschimbat până la limita de cristal (suprafață) la z = 0.
Figura 4.3 prezintă diagrama energetică a IPF. Valoarea potențialului electrostatic fără dimensiune pe suprafață este notată cu Ys. Semnul pentru această valoare, în conformitate cu direcția acceptată a citirii energiei, va fi pozitiv pentru curbele din zonele în jos și negative pentru curbele în sus.
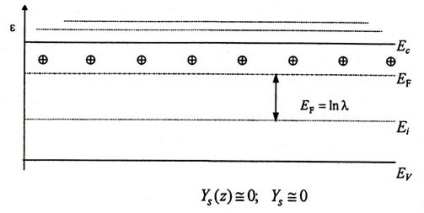
Fig .4.3. Diagrama energetică a regiunii de încărcare spațială a unui semiconductor cu tipul de conductivitate electronică pentru o valoare arbitrară a potențialului electrostatic de suprafață
Se vede clar din figură că, în prezența îndoirii zonei, valoarea energiei Fermi devine o funcție a coordonatei z. Prin urmare, este clar că pentru orice punct (sau secțiune transversală a unei suprafețe paralele) a SCR în conformitate cu legile statistice, expresia pentru concentrațiile de echilibru poate fi scrisă sub forma
Din considerațiile generale și considerând diagrama energetică din figura 4.3 se poate observa, energia Fermi la fiecare punct determinat de diferența Ys zone și energia Fermi în cea mai mare parte de îndoire
Acest lucru ne permite să notăm
Folosind formulele (4.1.7), obținem
Să analizăm pe scurt semnele EF și Ys introduse. Semnul potențialului electrostatic fără dimensiuni va fi negativ atunci când zonele sunt îndoite în sus și pozitive atunci când se îndoaie în jos. FE. și, de asemenea, Ys va avea un semn negativ dacă nivelul Fermi este pe diagrama energiei din jumătatea inferioară a benzii interzise și invers.
Relațiile (4.2.7) reflectă efectiv utilizarea statisticilor Maxwell-Boltzmann pentru a determina concentrațiile de suprafață ns și ps. A fost deja remarcat mai devreme că este foarte aproape de zona permisă. Factorul de proximitate este determinat de raportul dintre exponentul unității din numitorul cu formula (4.1.1). Dacă exponentul este mai mare de 3, atunci exponentul este un ordin de mărime mai mare decât unitatea - trecerea la statisticile lui Boltzmann. În caz contrar, degenerarea are loc și este necesar să se utilizeze statisticile Fermi.
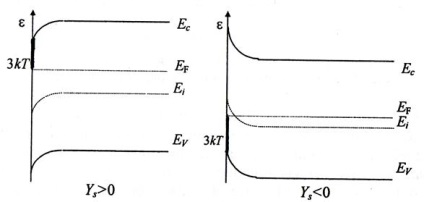
Fig. Diagrame energetice care ilustrează curburile zonei de limitare
Pentru suprafață aceasta înseamnă că vor fi luate în considerare astfel de curbe ale zonelor, sub care nivelul Fermi de pe suprafață nu se apropie de marginile zonelor admise cu mai mult de 2-3 kO T.
Limitele curbelor sunt prezentate în graficele din Fig.4.4
Să luăm în considerare diferite tipuri de HMOs apărute la interfețe, mai întâi calitativ, chiar înainte de a rezolva ecuația Poisson. De exemplu, să selectăm formarea unei SCR de suprafață pentru un semiconductor cu o conductivitate suficient de pronunțată de tip n. Aceasta înseamnă că inegalitatea EF = ln # 955;> 3 o ține pentru ea.
1. Zone plate. Această situație este reprezentată pe diagrama energiei cu zone directe până la suprafață (Fig.4.5). Poziția nivelului Fermi pe suprafață coincide cu cea din volum. Regiunea de încărcare spațială nu este formată: (Z) = 0
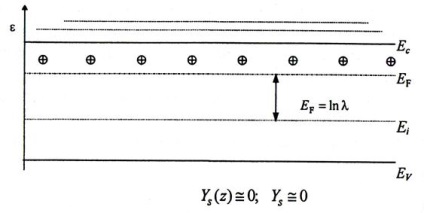
Figura 4.5. Diagrama energiei pentru cazul zonelor plate (regiunea spatiu-taxa absenta)
2. Îmbogățirea. Trebuie remarcat faptul că acești termeni și toți termenii ulteriori se referă la o schimbare a concentrației principalilor transportatori de taxe. De exemplu, în cazul în cauză, este clar că îmbogățirea înseamnă o creștere a concentrației principalilor purtători în suprafața OPZ. Această regiune a fost "îmbogățită" de principalii purtători de taxe - n (z)> n0. Pentru un semiconductor cu electroni selectat ca exemplu, aceasta înseamnă că nivelul Fermi la suprafață și în întreaga regiune de încărcare spațială este mai aproape de banda de conducție decât în vrac. Toate acestea corespund îndoirii zonelor în jos. În sistemul de referință ales, aceasta corespunde unei valori pozitive a potențialului electrostatic de suprafață - Ys> 0 (figura 4.6).
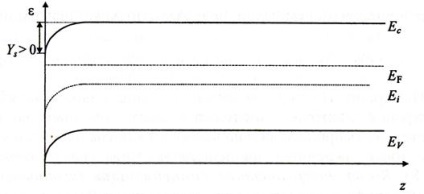
Figura 4.6. Diagrama energetică a suprafeței semiconductoare de tip n, corespunzătoare cazului de îmbogățire ns> n0
Dacă concentrația de suprafață ns nu este prea mare în comparație cu n0. atunci aceasta este o îmbogățire proastă. Aceasta corespunde curbelor Ys
Când Ys> 3, o îmbogățire puternică are loc atunci când ns >> n0. Este clar că atunci când îmbogățirea concentrației de găuri în regiunea de încărcare spațială este mai mică decât în volum, deoarece la echilibru este întotdeauna np = ni2.
3. epuizarea. În conformitate cu definiția de mai sus, această stare ar trebui să însemne că concentrația de electroni în SCR este mai mică decât în volumul n (z)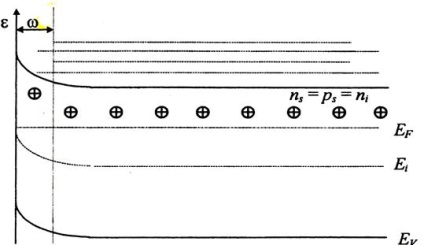
Figura 4.7. Schema energetică a suprafeței semiconductoare de tip n, care corespunde epuizării
Cu o creștere suplimentară a îndoirii zonelor, vine un moment în care concentrațiile electronilor și găurilor pot fi neglijate în comparație cu concentrația donatorilor ionizați. În consecință, acești donori imobiliari formează cea mai mare parte a încărcăturii de suprafață. Nivelul Fermi de pe suprafață coincide cu mijlocul banda interzisă pe suprafață Ys = ln # 955; Electronii, așa cum au fost, sunt mutați înapoi în volum cu o anumită adâncime W, care limitează stratul clar de epuizare (figura 4.7).
Raportul dintre volumul și concentrațiile de suprafață în acest caz
4. Inversiune. Pe măsură ce îndoirea negativă a zonelor crește, concentrația de electroni continuă să scadă, iar concentrația orificiilor crește. Acest proces este foarte accelerat după trecerea nivelului Fermi sub mijlocul benzii interzise pe suprafață (Fig.4.8)