Formula lui Hartley nu reflectă caracterul aleator al evenimentelor, deci în cazul general este necesar să se asigure o legătură între cantitatea de informații și probabilitatea apariției evenimentelor relevante (mesaje).
Această problemă a fost rezolvată în 1946 de către matematicianul american Claude Shannon.
Cu o abordare statistică (probabilă), informațiile sunt considerate drept o măsură a probabilității apariției unui mesaj corespunzător.
Din acest punct de vedere, cu cât este mai probabil evenimentul, cu atât mai puține informații din mesajul pe care îl avem despre el.
Multe tipuri de mesaje pot fi reduse la dublu.
În cazul general, un eveniment poate fi considerat rezultatul unui rezultat al unui experiment. Grupul complet al tuturor rezultatelor posibile de rezolvare a acestor situații se numește ansamblul de evenimente.
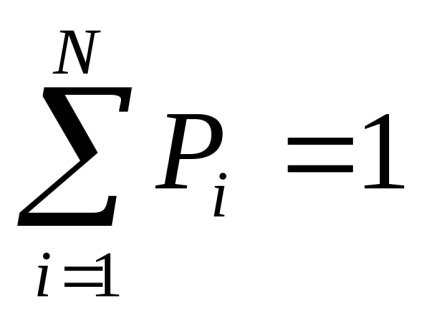
Fie numărul total al tuturor rezultatelor posibile N, din care K nu se repetă.
Apoi, probabilitatea unui eveniment i-th.
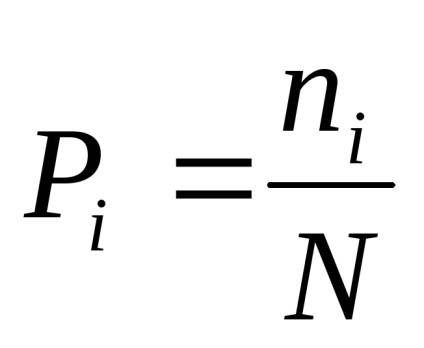
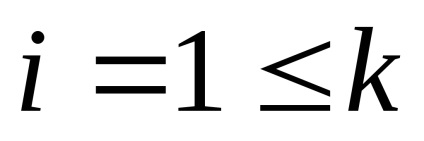
Fiecare implementare a acestui eveniment oferă o anumită cantitate de informații

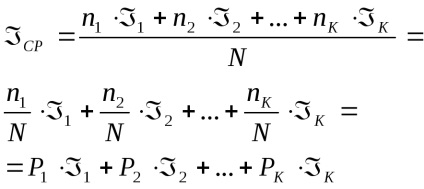
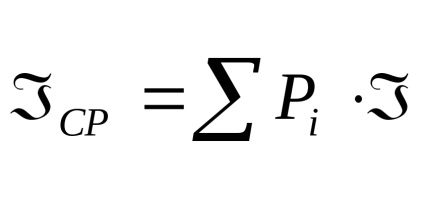
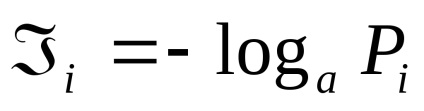
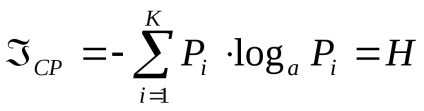
4 Măsurarea statică a informațiilor. Probabilitate și informații
Formula lui Hartley nu reflectă caracterul aleator al evenimentelor, deci în cazul general este necesar să se asigure o legătură între cantitatea de informații și probabilitatea apariției evenimentelor relevante (mesaje).
Această problemă a fost rezolvată în 1946 de către matematicianul american Claude Shannon.
Cu o abordare statistică (probabilă), informațiile sunt considerate drept o măsură a probabilității apariției unui mesaj corespunzător.
Din acest punct de vedere, cu cât este mai probabil evenimentul, cu atât mai puține informații din mesajul pe care îl avem despre el.
Multe tipuri de mesaje pot fi reduse la dublu.
În cazul general, un eveniment poate fi considerat rezultatul unui rezultat al unui experiment. Grupul complet al tuturor rezultatelor posibile de rezolvare a acestor situații se numește ansamblul de evenimente.
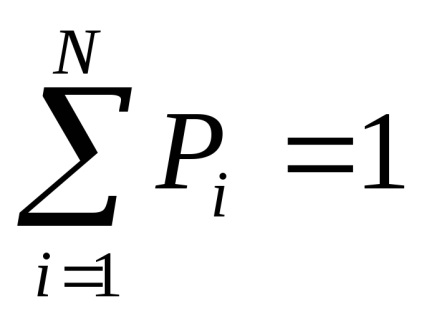
Fie numărul total al tuturor rezultatelor posibile N, din care K nu se repetă.
Apoi, probabilitatea unui eveniment i-th.
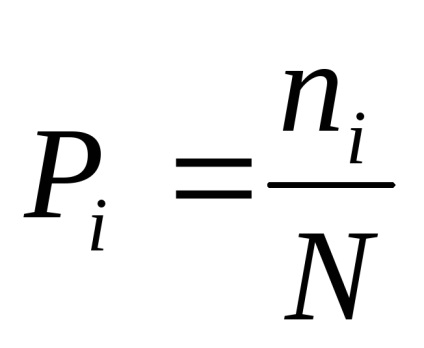
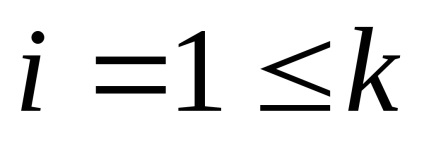
Fiecare implementare a acestui eveniment oferă o anumită cantitate de informații

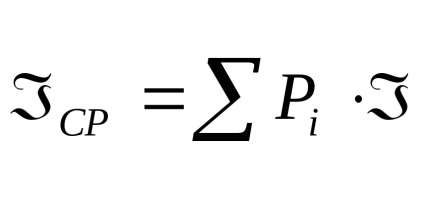
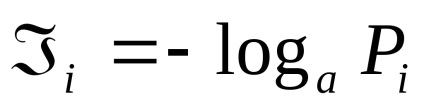
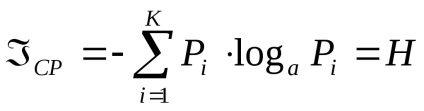
Proprietățile entropiei
1. Entropia este măsurată în aceleași unități ca și cantitatea de informații.
Semnul "-" din formula (2) înseamnă că entropia nu este întotdeauna negativă, adică
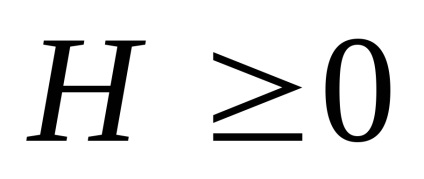
2. Entropia M atinge maximul dacă toate evenimentele sunt la fel de probabile.
3. H = 0 dacă probabilitatea unui eveniment i-a este 1.
Astfel, entropia este o măsură a incertitudinii comportamentului sursei de mesaje și caracterizează abilitatea acestei surse de a emite informații.
Odată cu creșterea numărului de stări posibile ale sistemului, energia crește.
În general, putem presupune că cantitatea de informații caracterizează scăderea entropiei ca urmare a procesului de cunoaștere.
Dacă incertitudinea este îndepărtată complet, cantitatea de energie este egală cu cantitatea de informații furnizată de sursă.
În cazul rezolvării incomplete a situației, cantitatea de informații este determinată de diferența dintre valorile inițiale și cele finale ale entropiei:
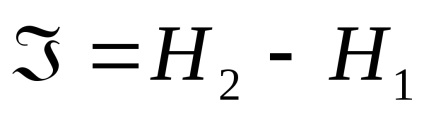
și anume Cantitatea de informații va fi determinată de diferența dintre valorile entropiei inițiale și cele finale.
Cea mai mare cantitate de informații este obținută atunci când incertitudinea este îndepărtată complet.
Evenimentele reale, precum și simbolurile în relații reale, nu sunt independente reciproc și echilibrate, care poartă de fapt fiecare simbol individual, vor fi mai mici decât valoarea maximă posibilă din punct de vedere teoretic.
Pierderea informațiilor se caracterizează printr-un factor de redundanță:
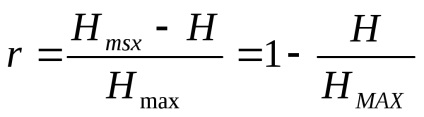
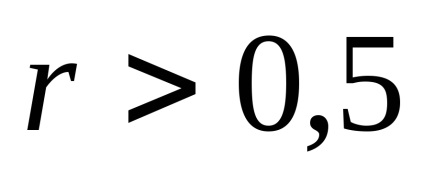
Pentru canalele de transmisie a informației, este utilizată o caracteristică denumită rata de date a canalelor, aceasta este egală cu cantitatea medie de informație care poate fi transmisă pe canalul de comunicație per unitate de timp.
Cantitatea medie de informație produsă de sursa mesajului pe unitate de timp se numește capacitatea sursei.
Rata maximă a datelor pentru un canal este numită lărgimea de bandă a canalului.
Problema potrivirii performanței surselor de semnal și a capacității canalului de transmisie este una dintre cele mai importante sarcini ale teoriei și practicii de codificare a informațiilor.