Soluția problemei de optimizare
Putem spune că functorul conjugat este o modalitate de a indica cea mai eficientă soluție a unei anumite probleme cu ajutorul metodei standard. De exemplu, o problemă elementară a teoriei inelelor - cum să transforme pseudoring (de exemplu, inel care poate avea o unitate de multiplicativ) în ring. Cel mai eficient mod de a face acest lucru - pentru a adăuga la unitatea de inel, toate elementele necesare pentru realizarea inelului de axiome (De exemplu, elementele de tip în cazul în care r 1 r. - element inelar) și nu sugerează nici relații noi în inelul care nu sunt necesare pentru a efectua axiome. Această construcție este standard în sensul că funcționează pentru orice pseudo-inel.
A spune că această metodă determină soluția "cea mai eficientă" și "standard" la o problemă este aceeași cu a spune că definește functorii conjugați.
Există mai multe definiții echivalente ale functorilor conjugați. Echivalența lor este elementară, dar nu banală.
Definiția cu ajutorul săgeții universale [⇨] este ușor de formulat, este și cea mai apropiată de intuiția noastră despre "problema de optimizare".
Definiția unei unități și a unei counit [⇨] este convenabilă pentru functorii care apar adesea în algebră, deoarece oferă formule care pot fi verificate direct.
Definirea cu ajutorul seturilor Hom [⇨] face simetria definiției evidente și clarifică motivele pentru denumirea functorilor ca fiind "conjugați".
Săgeată universală
Așa cum sugerează și terminologia, este adevărat că F - stânga Adjoint la G, dacă și numai dacă G - Adjoint dreptul la F. Cu toate acestea, nu este evident din definiția printr-o săgeată universală, dar, evident, din cauza definiției pe unitate și counit.
Unitate și coedit
numit consiliul și unitatea de conjugare, respectiv, astfel încât compozițiile
sunt transformările de identitate 1F și 1G ale functorilor F și G, respectiv.
Într-o astfel de situație, F este conjugat stânga pentru G și G este conjugat drept pentru F. Uneori această relație este notată (ε. Η). F ⊣ G sau pur și simplu F ⊣ G.
Sub formă de ecuații, condițiile de mai sus pe (ε, η) se numesc ecuațiile counit și unitate:
1 F = ε F ∘ F η 1 G = G ε ∘ η G 1 _ = \ varepsilon F \ F Circ \ eta \\ 1_ = G \ varepsilon \ Circ \ eta G \ end >>
Definiția prin functorul Hom
Aceasta determină familia bijecțiilor:
pentru toate obiectele X în C și Y în D.
Aici F se numește conjugatul stâng pentru G și G este conjugatul drept pentru F.
Pentru a înțelege ce se înțelege prin naturalitatea lui Φ. Trebuie să explicăm modul în care homC (F -, -) și HOMD (-, G -) sunt functori. De fapt, ambii sunt bifunctori de la D op × C la Set. Într-o formă explicită, naturalitatea lui Φ înseamnă că pentru toate morfismele f. X → X 'în C și morfismele g. Y '→ Y în D, urmărește următoarea diagramă:
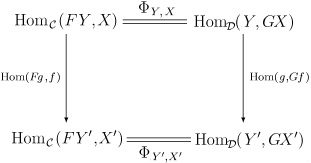
Grupuri libere
Designul unui grup liber este un exemplu convenabil pentru clarificarea esenței definițiilor. Să F. Grp ← Set - functor care asociază o pluralitate de grup liber Y generat de elementele și Y. G. Grp → Set - functorul uituci. care asociază lui X setul său de operatori. Apoi F este un conjugat stâng pentru G:
Săgeți terminale: pentru fiecare grupă X. grupul FGX este grupul liber generat de elementele lui X ca set. Să ε X. FGX → X: FGX \ X> - grupa omomorfismelor, care se traduce formând FGX în elementele corespunzătoare ale X. Atunci (G ε X. X))> - morfism terminalul de la F la X. deoarece orice homomorfism de liber grup FZ în X baleiază ε X. FGX → X: FGX \ X> cu o singură funcție a setului Z în X. set Aceasta înseamnă că (F, G) - o pereche de functori adjuncti.
Seturile Hom: mapările din grupul liber FY la grupul X corespund în mod univoc cu mapările setului Y în setul GX. fiecare omomorfism este determinat în mod unic de valorile sale pe generatorii unui grup liber. Prin calcul direct, se poate verifica că această corespondență este o transformare naturală și, prin urmare, perechea (F, G) este conjugată.
Alte exemple din algebră
Exemple din topologie
existență
unde indicele i rulez prin setul I. astfel încât orice morfism:
poate fi scris ca:
pentru unii în mine și un anumit morfism:
O declarație similară este caracterizată de functorii care au o conexiune dreaptă.
unicitatea
În direcția opusă, dacă F este conjugat la stânga lui G. și G este natural izomorf cu G '. atunci F este de asemenea conjugat la stânga lui G '.
compoziție
Compozițiile de conjugare pot fi luate într-un mod natural. Dacă este conjugat la stânga functoruluiTrecerea la limite
Articole similare