Obiectiv: studierea dependenței indicele de refracție al materialului prismatic de lungimea de undă a luminii incidentate.
Instrumente și accesorii: goniometru G-5, prisma, sursă de lumină.
Una dintre legile refracției luminii indică faptul că indicele de refracție al unei substanțe este o valoare constantă. Această lege a fost utilizată pentru a rezolva probleme practice legate de construcția căii unui fascicul de lumină în diverse instrumente optice. În rezolvarea acestor probleme nu a fost necesar să se specifice, avem de-a face cu un fascicul incident de lumină monocromatică sau (o singură culoare) are o compoziție complexă și conține valuri de lungimi diferite.
Trebuie remarcat totuși că atunci când un fascicul de lumină albă trece printr-o prisă triedulară, se descompune în părțile componente ale acestuia, formând un spectru continuu (figura 1). Prin urmare, lumina cu diferite lungimi de undă este refracționată în aceeași substanță în moduri diferite. Acest fenomen este cauzat de dependența de substanță a indicelui de refracție al lungimii de undă optice, se numește dispersia luminii, rezultând într-un prizmoyspektr rezultatedvukratnogo refractie se numește spectru de dispersie.
Dispersia luminii poate fi explicată pe baza teoriei electromagnetice și a teoriei electronice a materiei. Pentru a face acest lucru, trebuie să luăm în considerare procesul de interacțiune al unui val electromagnetic care trece prin materie, cu electroni în atomul materiei. Mișcarea electronilor într-un atom respectă legile mecanicii cuantice, iar analizarea acestei probleme prezintă dificultăți considerabile. Cu toate acestea, după cum arată Lorentz, pentru o înțelegere calitativă a multor fenomene optice este suficient să ne limităm la ipoteza existenței unei legături cvasi-elastice între electronii unui atom. Odată îndepărtați de la poziția de echilibru, astfel de electroni vor începe să oscileze, pierzând treptat energia vibrațiilor la radiația undelor electromagnetice. Ca urmare, oscilațiile vor fi amortizate, iar amortizarea poate fi luată în considerare prin introducerea unei "forțe de amortizare prin frecare" proporțională cu viteza.

roșu portocaliu galben verde albastru albastru violet
Când un val electromagnetic trece prin materie, electronul din atomul materiei este afectat de forța Lorentz din partea câmpului electromagnetic. Această forță este:
unde e - sarcina unui electron, - câmp electric; - viteza de electroni în substanță, - câmpul magnetic, - intensitatea câmpului magnetic asociat cu raportul de inducție (esli = 1).
Calculul arată că forța exercitată asupra electronilor de câmpul magnetic este de 4 ori mai puțin 10 decât rezistența câmpului electric, astfel încât al doilea termen din forța Lorentz poate fi neglijată și a considerat că acționează numai asupra forței de electroni de către câmpul electric. Deoarece această forță variază în conformitate cu legea armonică, aceasta este forța motrice, iar oscilațiile electronului sunt oscilații forțate.
unde 0 este faza inițială a oscilației electronului, determinată de coordonatele sale. E0 este amplitudinea forței câmpului electric și este frecvența ciclică a oscilațiilor vectorului în undele luminoase.
Pe lângă forța de forțare a electronului din atom, pe baza ipotezelor noastre simplificate, întoarcerea QUASI-
unde x este deplasarea electronului din poziția de echilibru, k este coeficientul de rigiditate și 0 este frecvența ciclică OWN a oscilațiilor electronului din atom.
Pentru a simplifica calculele, neglijăm amortizarea radiațiilor. Apoi, sub acțiunea acestor forțe, electronul din atom va efectua o mișcare oscilantă, ecuația diferențială care va avea forma:
Din teoria ecuațiilor diferențiale se știe că soluția (4) are forma: x = xmaxsin (⋅t + 0). unde amplitudinea
Să analizăm acum teoria dispersiei electronice. Pentru simplitate, presupunem că moleculele de materie sunt nepolare, adică moleculele sunt transformate în dipoli doar sub acțiunea unui câmp electric extern. În plus, deoarece masele nucleelor sunt mari în comparație cu masa electronilor, neglijăm deplasarea nucleelor din poziția de echilibru sub acțiunea undelor luminoase. În această aproximare, momentul electric dipol al moleculei poate fi reprezentat în forma: pi = exi max. unde xmax este deplasarea maximă a electronului i din poziția de echilibru sub acțiunea undelor electromagnetice. Deoarece electronii din moleculă au un set de frecvențe de oscilație naturale 0i. apoi substituind (5) în expresia momentului electric al dipolului moleculei, obținem:
Denumim numărul de molecule pe unitate de volum prin litera N. Produsul Np dă un vector de polarizare, care, după cum rezultă din teoria dielectricilor, este egal cu P = Np = EE. unde 0 este constanta electrică a vidului, este sensibilitatea dielectrică asociată cu permitivitatea dielectrică a substanței prin relația:
Deoarece indicele de refracție pentru dielectrice transparente, apoi de la
Așa cum se poate observa din (8), indicele de refracție al unei substanțe este o funcție a frecvenței luminii incidente (vezi figura 2), iar această dependență are un caracter de rezonanță. Cu alte cuvinte, la frecvențe semnificativ diferite de toate frecvențele naturale 0i electroni sumă (8) va fi mic în comparație cu unitatea, astfel încât n2 1. Indicele de refracție, în acest caz, crește cu frecvența luminii incidente ( 0) și dispersia se numește DISPERSIE NORMALĂ.
În apropierea fiecărei frecvențe proprii 0i, funcția (8) suferă o discontinuitate: când se apropie 0i din stânga, se transformă în + . când se îndreaptă spre dreapta-în- (linia punctată în figura 2).
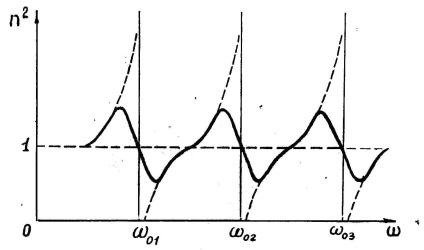
Acest comportament al funcției (8) se datorează faptului că am neglijat "fricțiunea prin radiație". Din teoria oscilațiilor rezultă că, în absența fricțiunii, amplitudinea oscilațiilor forțate devine infinită la rezonanță. Alocația pentru frecarea radiației conduce la dependența n2 de . prezentată în figura 2 printr-o curbă solidă. În regiunea 0i, indicele de refracție scade cu frecvență în creștere ( 0). Această regiune este numită regiunea DISPERZIUNII ANOMALE și corespunde absorbției de rezonanță a luminii de către materie.
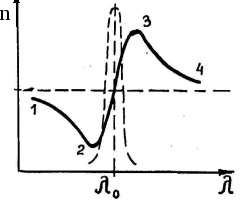
Trecând de la n2 la n și de la la . obținem curba n = f (), prezentată în figura 3 (este dată numai partea curbei în regiunea uneia dintre lungimile de undă rezonante 0i). Secțiunile curbei 1 -2 și 3 - 4 corespund zonei de dispersie normală ( 0), iar secțiunile 2 - 3 la dispersia anormală ( 0).
Pentru toate substanțele transparente incolore, funcția n = f () are un caracter în partea vizibilă a spectrului, prezentată în figura 3 prin secțiunea de curbă 3 - 4.
Așa cum se poate vedea din figura 3, pe măsură ce lungimea de undă a luminii trece prin substanță, indicele de refracție scade. Rezultă că razele purpurii suferă cea mai mare refracție în prisma triede, în spectrul de dispersie culoarea violetă va fi situată mai aproape de baza prismei.