Atunci când se efectuează un calcul al puterii, este necesar să se determine care parte a mecanismului este un sistem definabil din punct de vedere statistic.
Pentru sistemele determinate statistic, numărul de ecuații de statică trebuie să fie egal cu numărul de necunoscute. Indicăm prin n numărul de legături necunoscute ale mecanismului (plan), atunci numărul de posibile ecuații statice este 3n.
Determinăm numărul de necunoscute date de fiecare pereche cinematică a unui mecanism planic.
În mecanismele planare se utilizează perechi cinematice mai mari și inferioare din clasele a IV-a și a 5-a.
Perele cinematice din clasa a 5-a pot fi rotative și translaționale.
pereche cinematică rotativă din clasa a 5-a
Forțele, interacțiunile sunt distribuite conform unor legi de pe suprafața mecanismului, este obișnuit să fie reprezentat sub forma unui rezultat aplicat centrului balamalei. Punctul de aplicare este cunoscut, iar magnitudinea și direcțiile sunt necunoscute, prin urmare, perechea cinematică dă 2 necunoscute.
înainte de perechea cinematică a clasei a 5-a
Forțele de interacțiune sunt distribuite pe suprafețele de contact ale perechii și sunt reprezentate în mod obișnuit sub forma unui rezultat orientat perpendicular pe direcția de mișcare a mecanismului. În această pereche cinematică, direcția reacției este cunoscută, iar magnitudinea și punctul de aplicare nu sunt cunoscute, prin urmare, perechea dă 2 necunoscute.
pereche cinematică mai mare
În această pereche cinematică, reacția este îndreptată de-a lungul normalei, trasă la suprafața legăturilor prin punctul de contact. Sunt cunoscute direcția, punctul de aplicare și magnitudinea. Cu toate acestea, perechea cinematică mai mare poate fi înlocuită cu o pereche inferioară, deci putem presupune că numai perechile cinematice scăzute din clasa a 5-a sunt incluse în compoziția mecanismelor plane. Numărul de astfel de perechi climatice în mecanismul de P5 și fiecare va da 2 necunoscute. În consecință, toate necunoscutele sunt 2P5. O parte a mecanismului va fi definită static dacă 3n = 2p5 este satisfăcută pentru acesta. Acest raport corespunde grupului Assur, adică grupul Assur este un sistem determinat static și pentru acesta este efectuat calculul forței mecanismului.
11. Calculul forței grupului Assur II de categoria 1
1) Determinați forțele externe (momente) care acționează asupra legăturilor grupului asyrian. Mărimea acestor forțe este determinată din diagrama de sarcină. O clasă a grupului Assur este desenată pentru poziția examinată a mecanismului pe o scală. Definirea sarcinilor, forțelor și momentelor inerțiale:
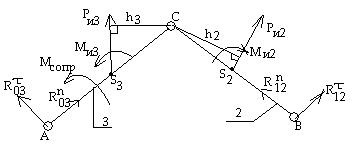
Calculul începe cu determinarea componentei tangente a lui R. din starea de echilibru a celei de-a doua legături folosind ecuația de momente în raport cu punctul C.
Determinăm reacția din starea de echilibru a linkului 3, folosind ecuația momentului pentru punctul E.
Se determină componentele normale ale reacției și din starea de echilibru a întregului grup asyrian, utilizând ecuația vectorului
Pentru a rezolva grafic ecuația vectorului, vom construi un plan de forțe pe o scară. Definiți segmentele pentru a construi forțele cunoscute pe plan.
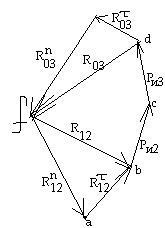
Pentru a determina reacția în balama C, vom scrie ecuațiile vectoriale ale echilibrului fiecăruia dintre legăturile din grup individual: