Referent S.S. Nycolaev
Zadorozhny N.A. Chuyev A.S. Sorokina L.A.
În partea teoretică a orientărilor se prezintă o descriere a efectului piezoelectric direct și invers, sunt prezentate caracteristicile diferitelor piezomateriale și domeniul de aplicare a acestora. Este prezentată o descriere a configurației de laborator și a procedurii de efectuare a experimentului. Sunt furnizate instrucțiuni pentru prelucrarea rezultatelor măsurătorilor.
Pentru studenții de la cursul de 2 ani de toate specialitățile MSTU. NE Bauman. Fig. Bibliografie. 1 nume.
Nicolae Antonovici Zadorozhniy Anatoly Stepanovich Chuev Larisa Alexandrovna Sorokina
Studiul efectului piezoelectric
Corrector Computer layout
Obiectivele lucrării sunt cunoașterea efectului piezoelectric și a aplicațiilor sale;
- studiul materialelor piezoelectrice;
- stabilirea abilității de a realiza experimentul și de a-și prelucra rezultatele.
În 1756, academicianul rus F. Epinus a constatat că atunci când un cristal de turmalină a fost încălzit, au apărut acuzații electrice pe fețe. Ulterior, acest fenomen a primit numele de efect piroelectric. F. Epinus a presupus că cauza fenomenelor electrice observate cu o schimbare a temperaturii este încălzirea inegală a celor două suprafețe, ceea ce duce la apariția solicitărilor mecanice în cristal. În același timp, el a subliniat că constanța distribuției poliilor la anumite capete ale cristalului depinde de structura și compoziția sa, astfel că F.Epinus sa apropiat de descoperirea efectului piezoelectric.
Efectul piezoelectric în cristale a fost descoperit în 1880 de frații și J. P. Curie observă apariția pe suprafața plăcilor tăiate într-un anumit mod de cristal de cuarț, încărcări electrostatice sub acțiunea solicitărilor mecanice. Aceste sarcini sunt proporționale cu stresul mecanic, schimbă semnul împreună cu el și dispar atunci când tensiunea este îndepărtată.
Formarea încărcărilor electrostatice pe suprafața unui dielectric și apariția polarizării electrice în interiorul acestuia ca urmare a solicitărilor mecanice se numește efect piezoelectric direct.
Împreună cu efectul piezoelectric direct, există un efect piezoelectric invers. Se compune din faptul că, într-o placă tăiată într-un anumit mod dintr-un cristal piezoelectric, apare o deformare mecanică sub acțiunea câmpului electric aplicat. Valoarea deformării mecanice este proporțională cu rezistența câmpului electric.
Să luăm în considerare aspectele teoretice ale piezoelectricității.
Disponibilitatea efectului piezoelectric într-un mediu deformabil, în strânsă legătură cu conceptul de polarizare dielectric, care reflecta anumite caracteristici ale comportamentului anumitor materiale, dielectricilor (în particular), atunci când sunt expuse la un câmp electric.
Fenomenul de polarizare a unui dielectric plasat într-un câmp electrostatic se datorează prezenței în el a sarcinilor electrice în particule și a părților lor individuale, capabile să se deplaseze elastic sub acțiunea unui câmp electric. Spre deosebire de electricitatea gratuită,
o taxă de izolare taxele inerente părților individuale ale atomilor și moleculelor dielectricilor capabile cu deplasabil lor purtătoare de material în materialul dielectric pe distante macroscopice asociat, formând dipoli electrici sau dipoli orientați de-a lungul câmpului disponibil. În acest caz, atomii sau moleculele rămân legate în structura întregii sau a părții izolate a rețelei cristaline.
Există două tipuri de polarizare: orientare și deformare. Prima se referă la moleculele polare, a doua la moleculele nepolare. În dielectricii solizi, ale căror laturi cristaline sunt construite din ioni pozitivi și negativi, se observă polarizarea ionilor.
În absența unui câmp electric extern, se observă o polarizare spontană în astfel de dielectrice; totalul momentului dipol electric al moleculelor este diferit de zero. Ioniile care intră în rețeaua cristalină a feroelectricilor pot fi ușor deplasate de acțiunea solicitărilor mecanice. Un efect piezoelectric direct constă în apariția încărcărilor electrice pe suprafețele cristalelor din anumite clase de simetrie sub acțiunea unei sarcini mecanice asupra lor.
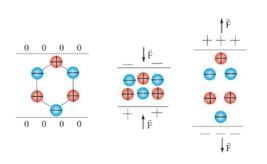
În absența solicitărilor mecanice externe, momentul dipolului electric al celulei unității este zero (figura 1). Dacă sub acțiunea unor astfel de tensiuni celulele sunt întinse sau comprimate, apare un moment dipol electric. Va fi
,
unde q este sarcina ionică și a este întinderea sau contracția celulară.
Prezența momentelor dipolului electric în interiorul piezoelectricului este detectată de apariția încărcăturilor electrice pe fețele opuse ale cristalului sau electrozilor piezoelementului (figura 1).
Fig.1. Schema de formare a efectului piezoelectric.
Amplitudinea sarcinii care apare când efectul piezoelectric este determinat de relația
unde: F x - magnitudinea forței care a determinat deformarea în direcția i; d jk este piezomodul (în forma generală, tensorul).
Este dovedit experimental că, în absența unui vector de câmp electric de polarizare a piezoelectric reprezentând o densitate în vrac a momentelor de dipol electrice asociate cu dependența mecanică liniară tensorului reprezentată prin următoarea relație:
P i = d ijk σ jk.
P i este componenta vectorului de polarizare P în direcția i;
σ jk este componenta tensorului de stres care apare în direcția perpendiculară; d ijk - modulele piezoelectrice în trei direcții reciproc perpendiculare.
Vectorul total de polarizare este dat de
P = P x + P y + P z.
Într-o formă simplificată, polarizarea poate fi reprezentată după cum urmează:
Tensorul de stres are o expresie matematică:
În noua notație, expresia pentru componentele de polarizare P ia
P X = d 11 σ 1 + d 12 σ 2 + d 13 σ 3 + d 14 σ 4 + d 15 σ 5 + d 16 σ 6
P Y = d 21 σ 1 + d 22 σ 2 + d 23 σ 3 + d 24 σ 4 + d 25 σ 5 + d 26 σ 6
P z = d 31 σ 1 + d 32 σ 2 + d 33 σ 3 + d 34 σ 4 + d 35 σ 5 + d 36 σ 6
Astfel, efectul piezoelectric este descris de o matrice cu participarea a 18 module piezoelectrice. Cu grad sporit de simetrie a cristalului, numărul de module care dispar este mai mare.
Apariția unui efect piezoelectric direct este ușor de înțeles cu ajutorul analizei modelului propusă de Meissner.
De exemplu, formula chimică a cuarțului este SiO. Grinzile sale cristaline constau din ioni de siliciu pozitivi și ioni negativi de oxigen. Dacă privim cristalul de-a lungul axei optice, aranjamentul ionilor arată astfel:
Când se comprimă de-a lungul axei X, se va observa un efect piezoelectric longitudinal.
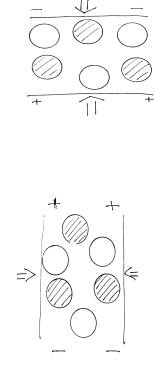
O schimbare în direcția comprimării duce la o schimbare a semnului încărcăturii de polarizare - se observă un efect piezoelectric transversal.
Pentru cuarț, piezomodulii sunt legați după cum urmează:
d 12 = - d 11 d 25 = - d 14 d 26 = - d 11
Deoarece toate celelalte module sunt 0, rămân doar două module independente
d 11 = 2,31 10-12 C / H d 14 = 0,7 10-12 C / H
Efectul piezoelectric în cuarț este descris de Eq.
= d 11 σ 1 - d 11 σ 2 + d 14 σ 4
= - d 14 σ 5 - d 11 σ 6
Piezoelectricitatea apare numai în acele cazuri în care deformarea elastică a cristalului este însoțită de o deplasare a centrelor de localizare a încărcărilor pozitive și negative ale celulei unice a cristalului, când induce un moment dipol individual, care este necesar pentru debutul polarizării electrice a unui dielectric sub acțiunea unei solicitări mecanice. În structurile având un centru de simetrie, nici tulpina uniformă nu poate perturba echilibrul intern al rețelei cristaline și, prin urmare, cristalele piezoelectrice sunt doar acele clase care nu dispun de un centru de simetrie. Absența unui centru de simetrie este
Este necesar, dar nu suficient, pentru existența unui efect piezoelectric, astfel încât nu toate cristalele acentrice îl posedă.
Efectul piezoelectric nu poate fi observat în dielectrice solide amorfe și criptocristaline (aproape izotropice), deoarece acestea contravin simetriei lor sferice. Singura excepție este atunci când acestea devin anizotropice sub influența forțelor externe și, prin urmare, dobândesc parțial proprietățile singurelor cristale.
Segnetoele ktri ki (numit primul material, in care efectul feroelectric a fost deschis -segnetova sare) - tvordyedielektriki (nekotoryeionnye ipezoelektriki cristale) având un anumit interval de temperaturi elektricheskimdipolnym impuls propriu, care poate fi reorientată domeniu datorită Apps vneshnegoelektricheskogo. Materialele feroelectrice posedă histerezisul momentului dipolului electric în raport cu câmpul electric aplicat. Mai mult, feroelectricilor au un anumit interval de temperatură, spontan polarizabilitate (spontan), t. E. polarizabilitate și în absența unui câmp electric extern.
În absența unui câmp electric extern este feroelectric, cum ar fi fost un mozaic de domenii - regiuni cu diferite direcții ale polarizării. În domeniile adiacente, aceste direcții sunt diferite și, în ansamblu, momentul dipol al dielectricului este zero. Atunci când face un feroelectric într-un câmp electric extern este reorientarea dipol momente ale domeniilor în domeniu, și astfel apărut total pe domeniu câmp electric va menține o parte din orientarea lor, precum și la terminarea câmpului extern. Prin urmare, feroelectricile au o permitivitate dielectrică foarte mare (de exemplu, pentru sarea Rochelle ε max ≈ 10 4).
Proprietățile feroelectrice ale substanțelor depind puternic de temperatură. Pentru fiecare feroelectric există o anumită temperatură deasupra căreia proprietățile neobișnuite dispar și se transformă într-un dielectric normal. Această temperatură se numește punctul Curie (în onoarea fizicianului francez Pierre Curie (1859-1906)). În mod tipic, feroelectricile au un singur punct Curie; singura excepție este sarea Rochelle (-18 și +24 ° C) și compușii izomorf cu aceasta. În cazul feroelectricilor din apropierea punctului Curie, se observă și o schimbare bruscă a căldurii specifice a materialului.
Până în prezent, efectul piezoelectric nu găsește o descriere cantitativă satisfăcătoare în cadrul teoriei atomice moderne a rețelei cristaline. Chiar și pentru structurile de cel mai simplu tip, nu se poate aproxima cel puțin ordinea constantelor piezoelectrice.
În prezent, a fost dezvoltată o teorie fenomenologică a efectului piezoelectric care corelează deformările și solicitările mecanice la câmpul electric și polarizarea în cristale. Se stabilește un sistem de parametri care determină eficiența cristalului ca piezoelectric. Principalii parametri ai piezoelectricilor sunt:
Modulul piezoelectric (modulul piezoelectric) dij - determină polarizarea cristalului (sau a densității de încărcare) pentru o anumită aplicație de încărcare mecanică;
constanta piezoelectrică - determină stresul mecanic care apare într-un cristal sub acțiunea unui câmp electric;
constanta piezoelectrica g - caracterizeaza tensiunea electrica in circuitul deschis la o anumita tensiune mecanica;
constanta piezoelectrica h - determina tensiunea electrica in circuitul deschis pentru o anumita deformare mecanica.
Aceste constante sunt cantități corelate și sunt legate între ele prin relații care includ constante elastice și permitivitatea cristalelor, astfel încât oricare dintre ele să poată fi utilizată. În practică piezomodulul este folosit cel mai adesea. Constantele piezoelectrice sunt tensori, prin urmare fiecare cristal poate avea mai multe piezomodule care caracterizează direcția deformării aplicate și mărimea încărcăturii electrice care apare.
Fiecare piezoelectric este un convertor de energie electromecanic, astfel încât caracteristica sa importantă este coeficientul de cuplare electromecanică r. Pătratul acestui coeficient este raportul dintre energia manifestată în forma mecanică pentru un anumit tip de deformare și energia electrică totală primită la intrarea de la sursa de energie.
În multe cazuri de aplicare practică a piezoelectricilor, proprietățile lor elastice sunt esențiale, care sunt descrise de modulul elastic - C (modulul lui Young - E 10) sau de valorile inverse - constantele elastice - S.
Atunci când se utilizează elemente piezoelectrice ca rezonatoare, în unele cazuri se introduce un coeficient de frecvență. care este un produs al frecvenței de rezonanță a elementului piezoelectric și dimensiunea geometrică care determină tipul de oscilație. Această valoare este proporțională cu viteza sunetului în direcția propagării undelor elastice în elementul piezoelectric.
În prezent, sunt cunoscute multe substanțe (mai mult de 500) care prezintă activitate piezoelectrică. Cu toate acestea, doar câteva dintre ele găsesc aplicații practice.
Quartz. Este un mineral foarte răspândit în natură, care la o temperatură sub 573 grade Celsius cristalizează în clasa trigonală-trapezoedală a syngoniei hexagonale. El aparține clasei enantiomorfe și se găsește în natură în două modificări: în dreapta și în stânga.
În compoziția chimică, cuarțul este o masă moleculară de silice anhidră (Si02) de 60,06 g / mol. Cuarțul este unul dintre cele mai solide minerale, are rezistență chimică mare.
Formele externe ale cristalelor de cuarț naturale sunt foarte diverse. Cea mai comună formă este combinația dintre prisma hexagonală și rhombohedra (fațete piramidale). Marginile prismei se extind până la baza cristalului și au o umbrire orizontală pe suprafață.
Cuarț, potrivit pentru utilizarea în echipamente piezoelectrice, se găsește în natură sub formă de cristale, fragmente și pelete. Culoarea cristalelor de cuart de la incolor-transparent (cristal de rock) la negru (morion).
În prezent, împreună cu cristale naturale de cuarț sintetic, crescute în autoclave, la temperaturi și presiuni ridicate, sunt utilizate soluții alcaline saturate cu alcalii.
Proprietățile piezoelectrice ale cuarțului sunt utilizate pe scară largă în tehnologie pentru stabilizarea și filtrarea frecvențelor radio, generând vibrații ultrasonice și pentru măsurarea cantităților mecanice (piezometrie).
Tourmaline. Turmalina cristalizează în clasa trigonală-piramidală a sistemului trigonal. Cristale prismatice cu umbrire longitudinală, alungită, adesea în formă de ac.
Conform compoziției chimice, turmalina este un aluminoborosilicat complex cu impurități de magneziu, fier sau metale alcaline (Na, Li, K).
Culoare de la negru la verde, de asemenea, roșu la un singur, mai puțin adesea incolor. Când fricțiunea este electrificată, are un efect piroelectric puternic.
Turmalina este distribuită pe scară largă în natură, dar în majoritatea cazurilor cristalele sunt pline de fisuri. Cristalele fără defecte potrivite pentru rezonatoare piezoelectrice sunt rare.
Sare de var. Sarea ferică cristalizează în clasa rombotetraedrică a syngoniei rombice. Aparținerea clasei enantiomorfe determină posibilitatea teoretică a existenței cristalelor drept și stâng de sare Rochelle. Cu toate acestea, cristalele de sare Rochelle, obținute din deșeurile de vinificație, sunt doar corecte.