În geometria proiectivă, o configurație pe un plan constă dintr-un set finit de puncte și o configurație finită de linii. astfel încât fiecare punct este incident cu un număr de linii și fiecare linie este incidentă cu un număr de puncte [2].
Deși unele configurații specifice au fost studiate anterior (de exemplu, Thomas Kirkmanom [en] în 1849), studiul formal al configurațiilor început Theodor Reye [en] în 1876, în cea de a doua ediție a cărții sale Geometrie der Lage (poziția geometrie), în contextul discuției teoremei lui Desargues. Ernst Steinitz a scris teza sa pe această temă în 1894 și configurații au fost polulyarizirovany în 1932 Hilbert și carte Cohn-Vossenom Anschauliche Geometrie (Geometrie și), care mai târziu a fost tradus în limba engleză [3].
Configurațiile pot fi studiate fie ca un anumit set de puncte și linii într-o anumită geometrie, cum ar fi euclidiană sau planul proiectiv (în acest caz se vorbește de implementare în această geometrie), sau ca o incidență abstractă geometrie. În acest din urmă caz, configurațiile sunt strâns legate de hipergrafele obișnuite și graficele bipartite biregulare [en] bipartite. dar cu constrângerea suplimentară - oricare două puncte ale structurilor de incidență pot fi asociate cu o singură linie maximă, și oricare două linii poate fi asociată cu un singur punct de maxim. Adică circumferința graficului bipartit corespunzător (graficul de configurare Lévy) trebuie să fie de cel puțin șase.
Configurația în plan este notat ca (pγℓπ), unde p - numărul de puncte, ℓ - numărul de linii, γ - numărul de linii care trec prin fiecare punct și π - numărul de puncte pe fiecare linie. Pentru aceste numere, relație
deoarece acest produs este egal cu numărul de incidente punct-la-linie (steaguri).
Configurațiile cu același simbol nu trebuie să fie izomorf ca modele de incidență. De exemplu, există trei configurații diferite (93 93) - configurația Papp și două configurații mai puțin vizibile.
În unele configurații, p = 1 și, prin urmare, γ = π. Acestea se numesc configurații simetrice sau echilibrate [4] și, de obicei, în notație repetarea este omisă. De exemplu, (93 93) este redus la (93).
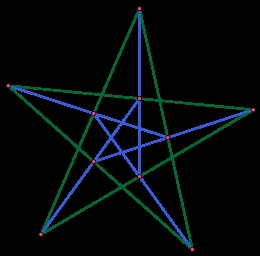
Configurația (103) care nu este izomorfă în ceea ce privește incidența configurației Desargues
Următoarele configurații proiective sunt cele mai vizibile:
- (11), cea mai simplă configurație posibilă, constând dintr-un punct pe o linie dreaptă. Din cauza trivialității, adesea nu este luată în considerare.
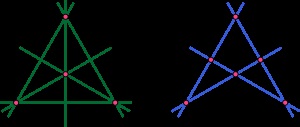
- (32), un triunghi. Fiecare dintre cele trei laturi conține două din cele trei noduri și invers. În general, orice poligon cu n laturi formează o configurație de tip (n2)
- (43 62) și (62 43), un patrulater completă și patrulaterală completă [1].
- (73), avionul Fano. Această configurație există ca o geometrie abstractă a incidenței. Dar nu poate fi construit pe planul euclidian.
- (83), configurația Mobius-Cantor. Această configurație este alcătuită din două cvadrilaterale, descrise și inscripționate simultan unul cu celălalt. Configurația nu poate fi construită pe planul euclidian, dar ecuațiile care o determină au soluții netriviale în numere complexe.
- (93), configurația Papp.
- (94 123), configurarea Hesse a nouă puncte de inflexiune a unui cubic pe planul proiectiv complex și douăsprezece linii drepte, fiecare dintre ele conținând trei puncte. Această configurație are aceeași proprietate cu planul Fano, și anume, că conține toate liniile care trec prin oricare două puncte ale configurației. Configurațiile cu astfel de proprietăți sunt cunoscute sub numele de configurații Sylvester-Gallai. Pentru aceste configurații, prin teorema Sylvester, nu pot exista coordonate în numere reale [5].
- (103), configurația lui Desargues.
- (125 302), dublul șase Schlafli. format din 12 din 27 de suprafețe cubice drepte [ro]
- (153), configurația lui Cremona - Richmond. Formată de 15 linii drepte care nu sunt incluse în planurile duble șase și cele 15 tangente
- (124 163), configurația Reye.
- (166), configurația Kummer [en].
- (273), configurația gri
- (6015), configurația Klein [en].
O configurație proiectiv duală pentru (pγlπ) este o configurație (lppγ) în care rolurile "puncte" și "linii" sunt schimbate. Prin urmare, configurațiile sunt perechi duale, cu excepția situației în care configurația duală este izomorfă celei originale. Aceste excepții se numesc configurații auto-duale, iar în aceste cazuri p = l [6].
Numărul de configurații nonisomorfe de tip (n3), începând cu n = 7, constituie secvența
Aceste numere sunt calculate ca modele de incidență abstractă, indiferent de posibilitatea implementării lor [7]. După cum scrie Gropp [8]. nouă din zece configurații (103) și toate configurațiile (113) și (123), permite punerea în aplicare în spațiul Euclidian, dar pentru orice n ≥ 16 are cel puțin o configurație irealizabilă (n3). GROPP indică, de asemenea, un bug în picioare lung în secvența - într-un articol în 1895 a fost o încercare de a lista toate configurația (123) și 228 dintre ei au fost găsite, dar configurația 229-lea nu a fost deschis până în anul 1988.
Construcția de configurații simetrice
Există mai multe metode pentru construirea de configurații, de obicei începând cu configurații deja cunoscute. Unele dintre cele mai simple dintre aceste metode construiesc configurații simetrice (pγ).
Orice plan proiectat finit al ordinului n este o configurație ((n 2 + n + 1) n + 1). Fie Π un plan proiectiv de ordine n. Eliminăm punctul P din Π și toate liniile Π trecând prin P (dar nu punctele situate pe aceste linii, cu excepția punctului P) și scoatem linia l. care nu trece prin P. și toate punctele situate pe această linie. Ca rezultat, obținem o configurație de tip ((n 2 - 1) n). Dacă alegem linia l în construcție. trecând prin P. obținem o configurație de tip ((n2) n). Deoarece se știe că există avioane proiective pentru toate ordinele n. care sunt puterile primelor, aceste construcții oferă o familie infinită de configurații simetrice.
Nu toate configurațiile sunt realizabile, de exemplu, configurația (437) nu există [9]. Cu toate acestea Group [10] a dat o construcție care arată că pentru k ≥ 3 configurație (pk) există pentru toate p ≥ 2 lk + 1, unde lk este lungimea optimale conducători Golomb ordine k.
Conceptul de configurație poate fi generalizat la dimensiuni mai mari, de exemplu pentru puncte și linii sau planuri în spațiu. În acest caz, restricția că nici două puncte nu se poate afla pe mai mult de două linii poate fi slăbită, deoarece două puncte pot aparține mai multor planuri.
În spațiul tridimensional,
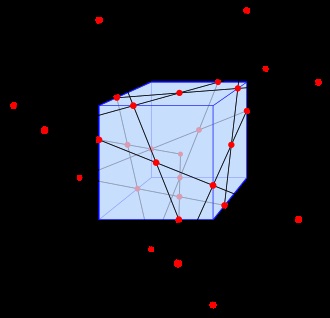
- Configurația Mobius. constând din două tetraedre inscripționate reciproc
- Reye configurație. alcătuită din douăsprezece puncte și douăsprezece planuri cu șase puncte pe fiecare plan și șase planuri care trec prin fiecare punct
- Configurația gri. constând din 27 de puncte de 3 × 3 × 3 și 27 de linii ortogonale care trec prin ele
- Dublul șase Shlefli. Se compune din 30 de puncte și 12 linii drepte, două linii drepte pe punct și cinci puncte pe o linie dreaptă.
O generalizare ulterioară se obține în spațiul tridimensional atunci când se ia în considerare incidența punctelor, liniilor și planelor, adică spațiile j pentru 0 ≤ j <3, где каждое j -пространство инцидентно Njkk -пространствам (j ≠ k ). Если обозначить через Njj число j -пространств, такую конфигурацию можно представить в виде матрицы :
Abordarea poate fi generalizată pentru alte dimensiuni n. unde 0 ≤ j
Articole similare