Construcția codurilor Hamming se bazează pe principiul verificării parității greutății W (numărul de simboluri unice) în blocul de informații al blocului de coduri.
Să clarificăm ideea de verificare a parității cu exemplul celui mai simplu cod de corecție, numit cod de verificare a parității sau cod cu paritate (egalitate).
Acest cod la combinații de cod binar bezizbytochnogo m primar - cod de biți adaugă un bit suplimentar (simbol de verificare a parității pe numita verificare sau de control). În cazul în care numărul de simboluri „1“ din cuvântul de cod original este chiar, descărcarea suplimentară generează un simbol pilot 0, iar în cazul în care numărul de simboluri „1“ este, apoi formând în continuare un simbol de descărcare 1. Ca urmare, numărul total impar de simboluri „1“ în orice cuvânt de cod transmis Acesta va fi întotdeauna chiar.
Astfel, regula pentru formarea unui simbol de verificare este următoarea:
,
unde i - simbolul de informații corespunzătoare (0 sau 1), m - și numărul total în exploatare „“ se referă în continuare la pomod2 plus. Este evident că adăugarea unei descărcări suplimentare crește numărul total de combinații posibile dublat comparativ cu numărul combinațiilor de coduri primare originale și împarte condiția de paritate este permisă pentru toate combinațiile și nerezolvate. Codul cu Paritatea poate detecta o singură eroare atunci când primesc un nume de cod, ca atare încalcă eroarea de paritate, traducerea permisă în combinație interzisă.
Criteriul corectitudinii combinației primite este egalitatea cu zero a rezultatului S al sumării mod2 a tuturor simbolurilor n a codului, inclusiv a simbolului de verificare k1. În prezența unei singure erori, S devine 1:
.
Acest cod este (m + 1, m) - cod, sau (n, n -1) - cod. Distanța minimă de cod este de două (dmin = 2) și, prin urmare, nu pot fi corectate erorile. Un simplu cod de verificare a parității poate fi folosit numai pentru a detecta (dar nu corecta) erorile individuale.
Creșterea numărului de cifre suplimentare de verificare și formarea simbolurilor de verificare k în anumite reguli. egal cu 0 sau 1, puteți consolida proprietățile corective ale codului, astfel încât acesta să vă permită nu numai detectarea, ci și corectarea erorilor. Aceasta este baza pentru construirea codurilor Hamming.
Codurile Hamming. Luați în considerare aceste coduri, care vă permit să corectați o singură eroare folosind o descriere directă. Pentru fiecare număr de simboluri de verificare k = 3,4,5 ... există un cod clasic Hamming cu marcajul
și anume - (7.4), (15.11), (31.26) ...
Pentru alte valori ale numărului m de simboluri de informații obținute prin așa numitele scurtate (trunchiate) codurile Hamming. Deci, pentru codul telegrafică internațional MTC-2. 5 având caractere de informații trebuie să folosiți codul de corecție (9,5) fiind trunchiat de cod Hamming clasic (15,11), deoarece numărul de caractere din acest cod este redus (prescurtat) la 6. De exemplu, să considerăm un cod Hamming (7,4 ), care poate fi format și descris de codorului prezentat în ris.13.1. În forma sa cea mai simplă pentru date de simboluri patru (m = 4) informații (I1, I2, I3, I4), presupunem că acestea sunt grupate împreună la începutul cuvântului cod, deși nu este obligatoriu. Supliment aceste simboluri de informare sunt paritate trei (k = 3), cerându-le următoarele ecuații Paritatea, care sunt determinate de algoritmi adecvați. Este cunoscut faptul că distanța de cod egal cu numărul minim de controale, care include simbolul de informații plus unu. În acest kodedmin. Prin urmare, fiecare simbol de informații trebuie să includă cel puțin două inspecții. Determinăm regulile de formare a parității, după cum urmează:
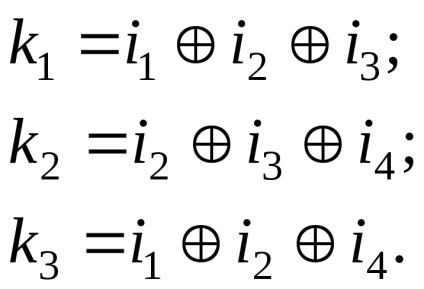
În conformitate cu acest algoritm pentru determinarea valorilor simbolurilor de paritate ki în figura 13.3, sunt enumerate toate cele 16 cuvinte de cod (7.4) posibile ale codului Hamming.
În Fig. Figura 13.2 prezintă circuitul de decodor pentru codul Hamming (7.4), al cărui intrare este un cuvânt de cod
.
Un apostrof înseamnă că orice simbol al unui cuvânt poate fi distorsionat de o interferență în canalul de transmisie.
În decodor, în modul de corectare a erorii, se construiește o secvență:

O secvență de trei caractere (s1, s2, s3) se numește sindrom. Termenul "sindrom" este de asemenea folosit în medicină, unde acesta denotă o combinație de simptome caracteristice unei anumite boli. În acest caz, sindromul S = (s1, s2, s3) este o combinație a rezultatelor verificării parității simbolurilor corespunzătoare grupului de coduri și caracterizează o anumită configurație de eroare (vector de eroare).
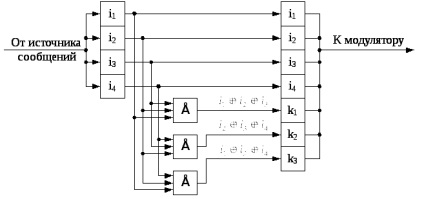
Ris.13.1. Coder pentru un cod simplu (7.4) - Hamming
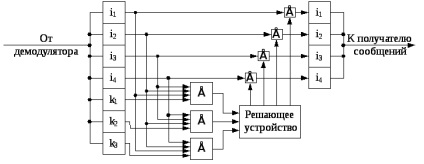
Ris.13.2. Decodor pentru codul simplu (7.4) - Hamming
Astfel, codul (7.4) vă permite să remediați toate singurele erori. O verificare simplă arată că fiecare dintre erori are propriul sindrom unic. Este posibil să se creeze un astfel de corector digital de eroare (decodorul sindromului), care corectează simbolul corespunzător în grupul de coduri recepționat pentru sindromul corespunzător. După corectare, simbolurile de verificare ki nu pot fi transmise la ieșirea decodorului (figura 13.2). Două sau mai multe erori depășesc capacitățile codului de corecție Hamming, iar decodorul va fi greșit. Aceasta înseamnă că va face corecții incorecte și va produce simboluri de informații distorsionate.
Ideea de a construi un astfel de cod de corecție, desigur, nu se schimbă atunci când rearanjați pozițiile de simboluri în cuvinte de cod. Toate aceste variante sunt de asemenea numite (7.4) Codurile Hamming.
Codurile extensibile ale lui Hamming sunt construite ca urmare a adăugării de coduri cu dmin = 3 printr-o verificare generală a fiecăreia dintre combinațiile de coduri pentru paritate, adică un alt simbol de control. Aceasta vă permite să măriți distanța minimă a codului la dmin = 4.
Pentru a continua descărcarea, trebuie să colectați imaginea: