Referințe. 15
Arramentele și listele legate definesc colecții de obiecte care sunt accesate secvențial. Aceste structuri de date sunt numite liste liniare, deoarece ele au elemente unice și ultime, iar fiecare element intern are un singur succesor. O listă liniară este o abstracție care vă permite să manipulați datele reprezentate în diverse moduri - arhiteuri, stive, cozi și liste legate.
În multe aplicații, este detectată o ordine neliniară de obiecte, unde elementele pot avea mai mulți moștenitori. De exemplu, în arborele genealogic părintele poate avea mai mulți copii (copii). În Fig. 1 arată trei generații ale familiei. Această ordonare este numită ierarhică.
În acest articol, vom examina o structură neliniară numită un copac care constă din noduri și ramuri și are o direcție de la rădăcină la nodurile exterioare numite frunze. Aceste structuri sunt similare cu rețeaua de comunicații prezentată în Fig. 2, necesită algoritmi specifici și sunt folosiți în aplicații speciale.
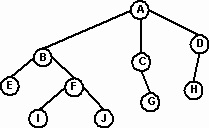
O structură de arbore este caracterizată de un set de noduri (noduri) care provin dintr-un singur nod inițial, numit rădăcină. În Fig. 3 este nodul A. În ceea ce privește arborele genealogic, nodul poate fi considerat un părinte care indică 0, 1 sau mai multe noduri, numite copii. De exemplu, nodul B este părintele fiilor E și F. Părintele nodului H este nodul D. Un copac poate reprezenta mai multe generații ale familiei. Fiii nodului și fiii fiilor lor sunt numiți descendenți, iar părinții și bunicii sunt strămoșii acestui nod. De exemplu, nodurile E, F, I, J - descendenți ai nodului B. Fiecare nod non-root are un singur părinte, iar fiecare părinte are 0 sau mai mulți fii. Un nod care nu are copii (E, G, H, I, J) se numește o frunză.
Fiecare nod arbore este rădăcina subtreei, care este determinată de acest nod și de toți copiii acelui nod. Nodul F este rădăcina subtreei care conține nodurile F, I și J. Nodul G este rădăcina subtreei fără descendenți. Această definiție ne permite să spunem că nodul A este rădăcina subtreei, care în sine se dovedește a fi un copac.
Trecerea de la nodul părinte la nodul copil și la alți copii se face de-a lungul căii. De exemplu, în Fig. 4 O cale de la rădăcină la nodul F se extinde de la A la B și de la B la F. Faptul că fiecare nod non-root are un singur părinte, se asigură că există o cale unică de la orice nod la copiii săi. Lungimea căii de la rădăcină la acest nod este nivelul nodului. Nivelul rădăcinii este 0. Fiecare fiu al rădăcinii este un nod al primului nivel, următoarea generație este nodurile celui de-al doilea nivel și așa mai departe. De exemplu, în Fig. 4 nod F este un nod al celui de-al doilea nivel cu o lungime de traiectorie de 2.
Adâncimea copacului este nivelul său maxim. Conceptul de adâncime poate fi, de asemenea, descris în termenii căii. Adâncimea arborelui este lungimea celei mai lungi căi de la rădăcină la nod.
În figura 4, adâncimea arborelui este de 3 cm.
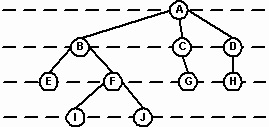
Figura 4. Nodul și lungimea căii
Deși copacii generali sunt destul de importanți, ne vom concentra pe o clasă limitată de arbori în care fiecare părinte nu are mai mult de doi fii (Figura 5). Astfel de copaci binari (copaci binari) au o structură unificată care permite diferite algoritmi de transmisie și acces eficient la elemente. Studiul copacilor binari face posibilă rezolvarea celor mai frecvente sarcini legate de arbori, deoarece orice copac de gen general poate fi reprezentat de un copac binar echivalent.
Fiecare nod al unui copac binar poate avea 0, 1 sau 2 fii. În raport cu nodul din stânga, vom folosi termenul stânga copil și în ceea ce privește nodul din dreapta este copilul potrivit. Numele "stânga" și "dreapta" se referă la reprezentarea grafică a arborelui. Un arbore binar este o structură recursivă. Fiecare nod este rădăcina propriului subordonat. El are fii care sunt ele înșiși rădăcinile copacilor, numiți substraturi stânga și dreapta, respectiv. Astfel, procedurile de prelucrare a copacilor sunt recursive. Iată definiția recursivă a unui copac binar:
Un arbore binar este un set de noduri B astfel încât
a) B este un arbore dacă setul de noduri este gol (un arbore gol este, de asemenea, un copac);
b) B este împărțit în trei subseturi disjuncte:
· Substratul din stânga R
· Subtitrul drept R
La orice nivel n, un arbore binar poate conține noduri de la 1 la 2n. Numărul de noduri per nivel este un indicator al densității arborelui. Intuitiv, densitatea este o măsură a dimensiunii unui copac (numărul de noduri) în raport cu adâncimea unui copac. În Fig. 5 Grafic A conține 8 noduri la adâncimea de 3, în timp ce graficul B conține 5 noduri la adâncime 4. Acest din urmă caz este o formă particulară, numită degenerat (degenerate) copac, care are o singură foaie (E) și fiecare nod non-frunză are doar un fiu. Un copac degenerat este echivalent cu o listă asociată.
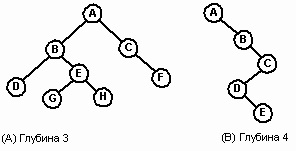
Figura 5. Copaci binari
Copacii cu densitate mare sunt foarte importanți ca structuri de date, deoarece ele conțin proporțional mai multe elemente în apropierea rădăcinii, adică cu căi mai scurte de la rădăcină. Un copac dens vă permite să stocați colecții mari de date și să accesați în mod efectiv articole. Căutare rapidă - principalul lucru care determină utilizarea arborilor pentru stocarea datelor.
Copacii degenerați reprezintă măsura supremă a densității. La cealaltă extremă - arborii binari complet (complet binar copac) adâncimea N, unde fiecare nivel este 0. N - 1 are un set complet de noduri și lasă toate nivelele N sunt situate în partea stângă. Un arbore binar complet care conține noduri 2N la nivelul N este complet. În Fig. 6 arborele binar complet și complet.
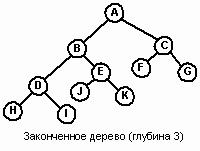
Figura 6. Clasificarea copacilor binari
Copacii binari sunt clasificați după câteva caracteristici. Introducem conceptele privind gradul unui nod și gradul unui copac. Gradul unui nod dintr-un arbore este numărul de arce care iese din el. Gradul arborelui este egal cu gradul maxim al nodului care intră în arbore. Pe baza definiției gradului, este clar că gradul nodului unui copac binar nu depășește două. În acest caz, frunzele din copac sunt vârfuri cu grad zero.

Figura 7. Arbore binar
O altă caracteristică importantă a clasificării structurale a copacilor binari este rigiditatea unui arbore binar. Un arbore binar strict constă numai din noduri care au gradul doi sau gradul zero. Un arbore binar absurd conține noduri cu un grad egal cu unul.

Figura 8. Arbori binari compleți și incompleți

Figura 9. Stricți și nu strict arbori binari
Copacii binari pot fi ușor reprezentați sub formă de liste sau matrice. Reprezentarea reprezentată a arborilor binari se bazează pe elementele corespunzătoare nodurilor copacului. Fiecare element are un câmp de date și două câmpuri de pointer. Un pointer este utilizat pentru a lega elementul de copilul drept, iar celălalt la stânga. Frunzele au indicii goale de descendenți. Cu acest mod de a reprezenta copacul, ar trebui să păstrați întotdeauna un pointer la nodul care este rădăcina copacului.
Puteți observa că acest mod de reprezentare are o asemănare cu listele liniare simple. Și această asemănare nu este accidentală. De fapt, modalitatea considerată de a reprezenta un arbore binar este un fel de multisesiune formată dintr-o combinație de seturi de liste liniare. Fiecare listă liniară combină nodurile care intră în calea de la rădăcina copacului la una din frunze.

Figura 10. Reprezentarea unui arbore binar sub forma unei structuri de listă
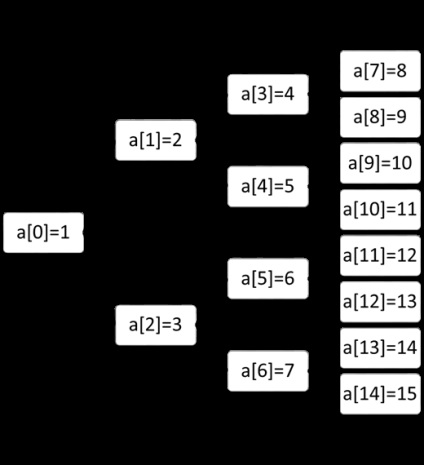
În forma unei matrice, arborele binar complet este cel mai ușor reprezentat, deoarece are întotdeauna un număr strict definit de noduri pe fiecare nivel. Vârfurile pot fi numerotate de la stânga la dreapta în mod succesiv prin nivele și pot utiliza aceste numere ca indici într-o matrice unidimensională.

Figura 11. Reprezentarea unui arbore binar ca matrice
Dacă numărul de nivele ale copacului nu se schimbă semnificativ în timpul procesării, atunci acest mod de reprezentare a unui arbore binar complet va fi mult mai economic decât orice structură de listă.
Principalul dezavantaj al modului considerat de a reprezenta un arbore binar este că structura de date este statică. Dimensiunea matricei este aleasă pe baza numărului maxim posibil de nivele ale arborelui binar. Și cu cât copacul este mai puțin complet, cu atât este mai puțin folosită memoria.
Ca un exemplu de folosire a unui arbore binar ca matrice, am folosit o matrice - a [i], constând din 15 elemente (de la 1 la 15). Ca rezultat, arborele ar trebui să arate ca: