Amploarea fracțiunii nu se modifică dacă numărul și numitorul fracțiunii sunt multiplicate cu același număr.
= =;
= =;
= =;
O astfel de transformare a unei fracțiuni se numește "extindere" a unei fracții. Fracțiunea se obține prin extinderea la 6 din fracție.
Dimensiunea fracțiunii nu se modifică dacă numărul și numitorul fracțiunii sunt împărțite în același număr.
O astfel de transformare se numește contracția unei fracții.
Cuvântul "procente" provine din latina "procento", ceea ce înseamnă "de la o sută".
Procentul reprezintă partea sute a numărului, notată cu%.
Orice număr întreg (de exemplu, 1) este de 100%. Partea ei sute este 1. 100 = 0,01. Prin urmare, 1% din unitate va fi 0,01.
Dacă în problemă valoarea totală este necunoscută și numai părțile sale sunt cunoscute, atunci este luată ca 100% sau 1 (unitate). Atunci când ansamblul constă din niște părți, atunci aceste părți sunt fracții, suma cărora este egală cu întregul (1). Proportional pentru aceste fracții o parte a întregului poate fi luată în procente.
Dacă întregul volum este de 100%, fiecare parte (fiecare fracțiune) este mai mare de 0%, dar mai mică de 100%, iar suma tuturor părților în procente este de 100%. Procentajul unei anumite valori este o fracțiune din această valoare, deci dacă 1 = 100%, atunci fiecare fracție (ordinară sau zecimală) este egală cu un procent din 1.
Exemplu: rotunjim până la cel de-al cincilea număr de 0,3442524.
Mii sunt a treia cifră după virgulă, ceea ce înseamnă că trebuie să ne uităm la a patra cifră:
0.3442 524 - în acest caz este de 2, așa că am rotunjit și am primit 0.344.
Amintiți-vă că cu cifrele de 0,1,2,3,4 rotunjite în jos. Cu cifrele 5,6,7,8,9 rotunjite. Deci, avem cinci cazuri și rotunjim la partea mai mică și mai mare.
Sarcinile de text # 8213; aceasta este una dintre sarcinile cele mai nefericite, mai ales pentru elevii de liceu, pentru că în continuare, cu cât este mai complicată starea, cu atât devine mai dificilă realizarea unei ecuații și rezolvarea corectă a problemei. Dar, ca și în orice subiect al matematicii, pentru a rezolva confidențial problemele complexe, este necesar să se facă față celor mai elementare tehnici.
Vom analiza aceste probleme încă de la început. Problema textului constă în situația în care este descrisă o anumită situație și întrebarea la care se răspunde răspunsul.
Exemplu: Kolya a lipit 2 autocolante pe 5 coli. Câte autocolante lipsea Kolya?
Stare: Kolya lipită pe 5 coli de 2 autocolante.
Întrebare: Câte stickere lipsea Kolya?
Soluția oricărei probleme de text poate fi împărțită în mai multe etape principale:
· Lucrul cu condiția;
· Se pot face multe condiții diferite pentru o ecuație.
Condiția 1: Masha și Petya au găsit împreună 5 ciuperci. Masha a găsit 2. Câte ciuperci a găsit Petya?
Conditia 2: Buchetul este format din musetel si clopote. În total sunt 5 flori în buchet, 2 dintre acestea sunt camomile. Câte clopote sunt în buchet?
Condiția 3: Pe copac erau 5 jucării. Doi dintre ei au căzut și s-au prăbușit. Câte jucării sunt lăsate pe copac?
Pentru a facilita lucrul cu condiția, este util să folosiți ilustrația sau modelarea. Aceasta poate fi o scurtă declarație a stării matematice sau verbale. Poate fi și un desen sau un tabel suplimentar.
Exemplu: Petya este mai mare decât Koli, Seryozha este sub Kolya. Cine este mai înalt?
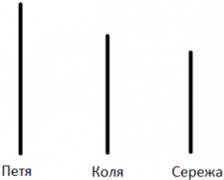
Din imagine, răspunsul este clar: Petya este mai presus de toate.
Pentru a compune ecuația în funcție de starea problemei, se folosesc diferite metode, în funcție de condiția de dependență a cantităților.
Această dependență este exprimată prin cuvinte: mai mare / mai mică, mai mare / mai mică, mai scumpă / mai ieftină, mai lungă / mai scurtă etc.
În formularea ecuației, prepozițiile "in" și "on" joacă un rol deosebit.
Exemplu: Petya este deasupra Kolya cu 20 cm, Serezha este sub Kolya cu 10 cm. Cati cm este Petya mai inalt decat Seryozha?
Soluție: Let Π # 8213; creștere Petit, K # 8213; creșterea lui Koli, C # 8213; creșterea Seryozha.
Apropo, acordați atenție acestei metode # 8213; alegeți variabilele "vorbind", și nu jocurile X și Yi fără chip, pentru a nu deveni confuze atunci când lucrați cu ecuația.
Exprimăm creșterea băieților.
Petya este deasupra Koli la 20 cm: P - 20 = K.
Serezha de sub Kolya la 10 cm: K = C + 10.
Înlocuim creșterea lui Koli în prima ecuație: П - 20 = С + 10.
Trebuie să aflăm cât de departe este Petya deasupra Seryozha: P - S.
Avem că Petya este cu 30 cm mai înaltă decât Seryozha.
Exemplu: La lecția de lucru, elevii au făcut fulgi de zăpadă. Au fost realizate în total 12 fulgi de zăpadă. Masha a făcut de două ori mai multe fulgi de zăpadă decât Kolya. Kolya a făcut 4 fulgi de zăpadă mai puțin decât romii. Câte fulgi de zăpadă a făcut-o pe Masha?
Să presupunem că M # 8213; numărul de fulgi de zăpadă pe care Masha la făcut, K - fulgii de zăpadă din Koli, R # 8213; fulgi de zăpadă Roma.
Masha a făcut de două ori mai multe fulgi de zăpadă ca Kolya: K = M / 2.
Kolya a făcut 4 fulgi de zăpadă mai puțin decât Roma: P = K + 4 = M / 2 + 4.
Împreună, băieții au făcut 12 fulgi de zăpadă: M + K + P = 12.
Substituim toate valorile exprimate prin M: M + M / 2 + M / 2 + 4 = 12.
Masha a făcut 4 fulgi de zăpadă.
procent # 8213; este întotdeauna o fracțiune de număr.
100% # 8213; tot numărul;
50% # 8213; jumătate;
25% # 8213; trimestru.
Pentru a găsi 1%, trebuie să împărțiți întregul număr cu 100.
1% din toate merele # 8213; = 1 măr.
1% din toate perele # 8213; = 2 pere.
Pentru a lucra cu procente, se utilizează proporția, în care valorile reale sunt scrise într-o coloană, în alta # 8213; interesul corespunzător.
200 de pere # 8213; 100%;
Progresia reflectă dependența cantităților. În alt mod se poate scrie sub forma a două fracții:.
Bazându-ne pe regulile de lucru cu fracțiunile, avem regulile de lucru cu proporția:
· Puteți reduce valorile într-o singură fracțiune.
· Produsul valorilor încrucișate este de 200 # 8729; 1 = 2 # 8729; 100.
Acest subiect va fi discutat în detaliu în curs.
De asemenea, sarcinile de text pot fi dedicate progreselor, productivității, ritmului # 8213; despre toate astea vom vorbi despre cursul nostru. Și începeți acum sarcinile de pregătire.
trapez # 8213; Este un patrulater cu două laturi opuse paralele.
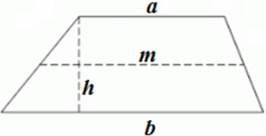
h # 8213; înălțimea trapezoidului (distanța dintre baze);
m # 8213; linia de mijloc a trapezoidului (segmentul care leagă mijlocul laturilor laterale ale trapezoidului).
Linia de mijloc a trapezoidului este egală cu jumătate din suma bazelor: m = și paralel cu acesta:
1) Rectangular # 8213; trapezul având unghiuri drepte pe partea laterală:
Partea este înălțimea.
2) Isoscele # 8213; trapezoid, în care laturile sunt egale:
· Unghiurile de la baza sunt egale
· Lungimile diagonalelor sunt egale cu
Suma unghiurilor interne ale trapezoidului (ca și a oricărui patrulater) este de 360 °.
· Suma unghiurilor adiacente lateral este de 180 °.
· Un cerc poate fi înscris în trapezoid dacă suma bazelor trapezoidului este egală cu suma laturilor sale laterale.
· Dacă trapezoidul poate fi înscris într-un cerc, atunci trapezoidul # 8213; isoscel.
· Despre un trapez izoscel, se poate descrie un cerc.
S = m # 8729; h. unde m # 8213; linia trapezului de mijloc.