Metoda de căutare pentru rezolvarea ecuațiilor cubice a primit cea mai mare faimă.
Metoda de căutare pentru rezolvarea ecuațiilor cubice a primit cea mai mare faimă. Algoritmul de implementare a acestuia este următorul.
Mai întâi, vom selecta una dintre rădăcinile ecuației folosind proprietatea că ecuația cubică conține invariabil cel puțin o rădăcină reală. și rădăcina integrală a ecuației cubice cu coeficienți întregi este un divizor al termenului liber d.
Coeficienții acestor ecuații. De regulă, ele sunt alese astfel încât rădăcina necesară este un număr întreg. cum ar fi: 0, ± 1, ± 2, ± 3.
Și, prin urmare, este necesar să găsim rădăcina printre aceste numere și să o verificăm prin substituire în ecuație.
Să luăm această rădăcină ca x 1.
În următoarea etapă, împărțim polinomalax 3 + b x 2 + cx + d prin binomul x - x 1.
Aplicăm teorema Bezout (împărțirea unui polinom într-un binomial liniar), conform căreia această divizare fără rest este posibilă, iar prin rezultatul calculelor obținem un polinom de gradul doi. care este zero. Rezolvarea ecuației pătratice obținute. vom găsi (sau nu!) celelalte două rădăcini.
Să analizăm cursul soluției ecuației: x 3 - 3x 2 - 13x + 15 = 0.
Vom găsi prima rădăcină, substituind cifra 0, ± 1, ± 2, ± 3 în ecuație, obținem că 1 este o rădăcină. Apoi, împărțim partea stângă a acestei ecuații cu binomul x-1 și obținem:
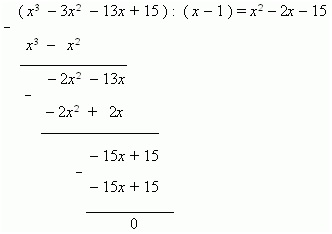
Apoi, calculați rădăcinile ecuației patrate. x 2 - 2x - 15 = 0.