Mi-a plăcut sarcina, pentru că simplu, dar nu bine purtat (nu am întâlnit altele similare).
Planul de soluții este următorul:
Ar trebui să apară imediat. Pentru utilizatorii neînregistrați cache-ul este utilizat timp de 1 oră, pentru utilizatorii înregistrați este dezactivat automat. Dar există și cache în partea de browser.
Multe mulțumiri! Asigurați-vă că ați stabilit soluția. -)
2) Dacă T este mai mică decât timpul de salt (care este probabil implicit), atunci este mai ușor să decideți acest lucru:
altfel întrebarea nu are sens.
4) scrieți ecuații cinematice de mișcare pe aceste axe (nu uitați de proiecțiile g care nu sunt zero);
nu este clar de ce ecuațiile cinematice ale mișcării ar trebui să fie compuse dacă exprimăm viteza prin legarea componentelor vitezei orizontale și verticale prin timpul t în SC selectat pe Soare.
5) Din ecuația cinematică, găsiți viteza la momentul potrivit T în proiecție pe axa perpendiculară pe direcția spre soare,
nu va fi aceasta o componentă verticală a vitezei?
2) a. Apoi, viteza este 0. Soluția totală trebuie să specifice viteza în funcție de T. Dacă T este mai mică decât timpul de zbor și viteza este 0. dacă este mai mare.
4) înseamnă o ecuație pentru viteză.
5) Va fi aceasta o componentă verticală a vitezei?
Dacă axa este în soare OY. Este perpendicular pe OX. atunci aceasta va fi proiecția pe axa OX. Deoarece axa OX nu este verticală, nu va fi o componentă verticală.
Și din nou: în ceea ce privește rezolvarea erorii am avut: a trebuit să scriu nu 1 / cos φ. dar 1 / sin φ.
Se scrie ecuația pentru variația coordonatelor de-a lungul axei X.
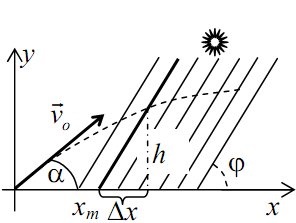
Coordonarea sfârșitului umbrei va fi determinată de expresia:
xm = x - δx = vo t cos α - h / tan φ.
unde h este înălțimea ascensiunii lăcustului la momentul t.
h = vo t sin sin α - gt 2/2.
Efectuând schimbarea în ecuație coordonatele umbrei:
xm = (vo cos α - vo sin α / tan φ) × t + gt2 / (2tg φ).
Diferențiând ecuația coordonatelor timpului, găsim legea schimbării vitezei umbrei lăcustului din timp: