Teoria sistemelor automate de control
Dacă un sistem automat funcționează simultan semnalul util și zgomot, problema optimă a sistemului de calcul apare pentru a obține cea mai mică eroare rezultată. Din punctul de vedere al semnalului dorit cel mai bun sistem de reproducere trebuie să aibă o lățime de bandă la fel de mare ca cel mai bun din punct de vedere al sistemului de suprimare a zgomotului, prin contrast, ar trebui să aibă o lățime de bandă mai mică posibilă. Criteriul pentru obținerea soluției optime aici este valoarea minimă a erorii de sistem rezultată, determinată de semnalul util și interferența.
Pentru variabilele aleatoare, este foarte simplu să se determine eroarea rădăcină medie-pătrată și, prin urmare, este utilizată pentru a estima precizia unui sistem automat.
Luați în considerare calculul sistemului bazat pe criteriul erorii minime rădăcină medie-pătrată cu acțiunea simultană a unui semnal util și a interferenței.
Conform acestui criteriu, inadecvarea erorii este proporțională cu pătratul amploarea sa. O astfel de afirmație este adesea logică, dar, desigur, nu se poate califica pentru o universalitate totală. În unele cazuri, de exemplu, atunci când fotografiați pentru orice scop, toate erorile mai mari decât o anumită valoare sunt la fel de nedorite. Cu toate acestea, eroarea medie pătrată a sistemului de control
în aproape toate cazurile este valoarea cea mai simplă calculată, care a determinat utilizarea acestui criteriu.
Sunt posibile mai multe formulări ale problemei. Cea mai simplă problemă poate fi formulată după cum urmează. Dacă există orice sistem de control automat al unei anumite structuri, este necesar să se aleagă parametrii sistemului pentru a obține minim eroarea pătratică medie pentru proprietățile statistice date ale semnalului dorit și interferențe.
Această problemă este rezolvată după cum urmează. Prin densitatea spectrală a erorii, prin integrarea sa, se constată dispersia. Dispersia se obține în funcție de caracteristicile probabilistice ale semnalului util, de interferență și de parametrii sistemului. Apoi, se caută condiții care trebuie suprapuse pe parametrii sistemului pentru a obține minimul varianței. Cu o expresie destul de simplă pentru varianță, aceasta poate fi determinată prin diferențierea directă și echivalând derivatele parțiale la zero.
În cazuri mai complexe, este necesar să căutăm minimul varianței prin setarea numerică a parametrilor de interes și construirea grafurilor corespunzătoare, precum și calcularea calculatorului.
printr-o formulă de transformare
- problema diferențierii, pentru H
- anticiparea statistică (predicție) și așa mai departe.
Eroarea de mai sus a sistemului poate fi reprezentată în formular
Este funcția de greutate a unui sistem închis.
Substituind (11.130) și (11.131) în formula (11.129), obținem
Problema este găsirea funcției de transfer de frecvență a unui sistem închis asociat funcției de greutate prin transformarea Fourier
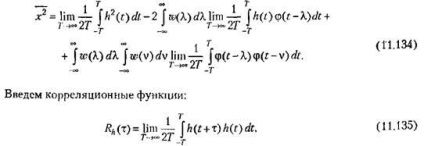
Deschidem parantezele din (11.132) și schimbăm ordinea de integrare:
Drept rezultat, expresia (11.134) poate fi transformată în formă
atunci limitele inferioare ale integrării în (11.138) trebuie să fie egal cu zero. Ca rezultat, ajungem
Ultima expresie arată că funcția de greutate optimă corespunzătoare minimului pătratului mediu al erorii este determinată numai de forma funcțiilor de corelare a semnalului util și a interferenței.
Se poate demonstra [88] că o condiție necesară și suficientă pentru minimizarea expresiei (11.139), care ar trebui să fie impusă funcția de ponderare este faptul că aceasta este soluția ecuației integrale Viiera-Hopf
Funcția de transfer optim (11.133) corespunzătoare funcției de ponderare optimă, care este soluția ecuației (11.140), poate fi reprezentat ca
adică în așa-numitul caz de netezire optimă, avem
În acest caz, soluția (11.1-11) poate fi reprezentată într-o formă mai simplă:
Numerotatorul acestei expresii este definit după cum urmează. Luați în considerare următoarea expresie:
-
Atunci când funcția optimă de transfer este realizată în sistem, se obține minimul teoretic al erorii pătrate medii. Acest minim este dat de
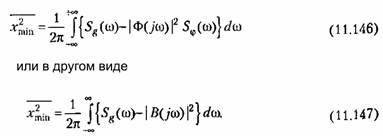
Să luăm în considerare un exemplu ilustrativ. Să presupunem că un semnal util u
interferența la intrarea sistemului corespunde densităților spectrale:
Dacã densitatea spectralã corespunde cu (11.136):

Îndepărtând primul termen din paranteze corespund polii în jumătatea inferioară, găsiți numărătorul funcției de transfer dorit (11.143):

Găsirea funcției de transfer optim nu înseamnă că sistemul real automat poate fi realizat în mod optim, deoarece implementarea sa poate fi dificilă. Funcția optimă de transfer, cu excepția cazurilor cele mai simple, ar trebui considerată o funcție ideală, la care totuși trebuie să se străduiască să facă acest lucru atunci când realizează un sistem automat real. Teoria sistemelor optime este prezentată în [22, 88, 89].