Să luăm în considerare principalele caracteristici ale problemei CT utilizând exemplul tomografiei de transmisie.
Ne limităm la problema avionului - când structura spațială a unui obiect este descrisă printr-o funcție a două coordonate, iar reconstrucția sa este realizată de un set de funcții (proiecții) dintr-o variabilă.
Lăsați un planar de raze X cu intensitate I0 să treacă prin obiect (vezi figura 1) în planul (X, Y). Să presupunem că S
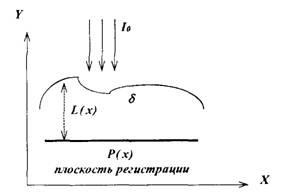
Fig. 1. Schema de tomografie de transmisie
printr-un mediu absorbant. Să presupunem că coeficientul de atenuare în obiect este constant: 8 (y) = c> "= const.
Apoi, sarcina cea mai simplă de tomografie (problema inversă) este obținerea formei obiectului și a valorii lui Sg prin funcția I (x).
Când un strat mic al mediului absorbant trece prin A, modificarea intensității radiației este proporțională cu grosimea acestui strat și cu coeficientul de amortizare:
Dacă integram (1) de-a lungul coordonatelor verticale de-a lungul fiecărei raze care formează secțiunea transversală a fasciculului, obținem imaginea obiectului în planul de înregistrare:
Expresia (2) formează baza tomografiei de transmisie: din funcția cunoscută F (x) este necesară obținerea funcției g (y) # 9632; Pentru S (y) = S0 = const, integrarea (2) produce.
Chiar și în acest caz, mai simplu este posibilă soluția problemei numai în anumite condiții: pentru a obține forma obiectului (funcția L (x)) trebuie să cunoască valoarea factorului de atenuare sau, invers, pentru a găsi coeficientul de atenuare necesar să se cunoască forma obiectului. În plus, în această formulare a problemei există un număr infinit de obiecte care în planul de înregistrare dau aceeași proiecție P (x). Într-adevăr, dacă limita inferioară a obiectului nu este plană, atunci fiecare funcție de grosime L (x) corespunde unui număr infinit de obiecte de forme diferite. În cazul în care iradiază obiectul dintr-un unghi diferit, proiecția în planul de înregistrare va fi diferit, dar problema ambiguitatea restaurării obiectului rămân. Astfel, restaurarea unui obiect ne cere să obținem informații despre proiecțiile obținute din diferite unghiuri. Trebuie să presupunem în prealabil că obiectul este un corp cu un coeficient constant de amortizare în interiorul acestuia. Sau avem nevoie de un număr mult mai mare de imagini ale obiectului. În consecință, pentru a rezolva problema inversă, avem nevoie de informații a priori (a priori - în latină - "de la precedentul"). Această proprietate este posedată de majoritatea absolută a problemelor de tomografie. În matematică, aceste probleme sunt numite nepotrivite [17]. Proprietățile lor de bază - ambiguitatea deciziei, precum și faptul că infinit mici erori în datele inițiale pot duce la erori în rezultatul final al calculelor [7, 11]. Un exemplu simplu: mici schimbări în coeficientul de amortizare S (v) în expresia (2), datorită integrării fasciculului L (\) poate conduce la schimbări semnificative în înregistrarea imaginii planul P (x).
Dezvoltarea metodelor de rezolvare a problemelor inverse este o mare parte a fizicii matematice moderne și a matematicii discrete. În aplicații practice, astfel de studii teoretice permit crearea de scheme optime de scanare pentru diferite tipuri de tomografie [6, 14]
În plus față de tomografia de transmisie examinată, tomografia de emisie a fost utilizată pe scară largă. Se utilizează în medicina nucleară, optică și radioteplotare (radiometrie) [5, 14]. Spre deosebire de tomografie cu emisie este că acesta este un exemplu tipic de măsurare pasiv - pentru a prelua informații despre obiectul este utilizat de propria radiație (raze X, optice, cuptor cu microunde), [5, 14]. De exemplu, în medicina nucleară, sarcina constă în găsirea distribuției spațiale a preparatului radioactiv în interiorul corpului în funcție de intensitatea radiației măsurată în afara corpului. La fel ca toate problemele de undă de detectare pasiv, această sarcină este mai complicată a discutat mai sus, în cazul planar, în locul expresiei (2), în planul imaginii de înregistrare va arata ca:
unde a este coordonata actuală a sursei de radiație, F
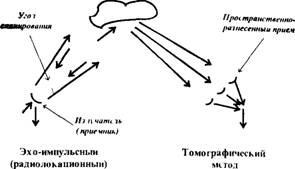
Figura 2 Diferența echo-pulsului de la metoda tomografiei de sondare
Tomografia acustică (AT) se bazează pe rezolvarea problemelor inverse de dispersie și refracție.
Diferența dintre tomografia acustică și metoda tradițională de sonorizare cu ecou-puls (radar) cu ultrasunete este prezentată schematic în Fig. 2.
În ambele cazuri, se presupune o scanare unghiulară a obiectului, cu toate acestea, pentru reconstrucția structurii sale prin metoda tomografiei, este necesară recepția spațială a semnalelor acustice. Cel mai adesea în AT, se folosește aproximarea optică geometrică (aproximarea razei). În acest caz, sursa de informații despre mediu nu este factorul de amortizare, ci viteza de propagare a sunetului. Problemele inverse ale împrăștierii și refracției din punct de vedere fizic diferă doar prin natura neomogenității și prin aproximările utilizate (figura 3).
Neomogenitatea mediului în propagarea de valuri de orice natură de-a lungul direcției # 1141; este determinată de schimbarea spațiului
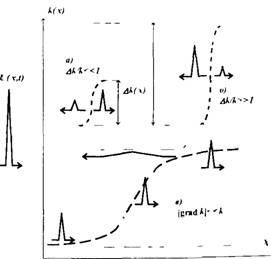
Fig.1 Variante de bază ale împrăștierii undei într-un mediu neomogen
unde ω este frecvența ciclică și c (n) este viteza de propagare a undelor. În cazul în care dimensiunile inhomogeneity sunt comparabile cu lungimea de undă, apoi un val reflectat, a cărui amplitudine este determinată de viteza și discontinuă, respectiv, numărul de undă DA (g) (partea superioară a fig. 3). Sub condiția A k / k «1, energia tranzitorii
poziția spațială a fiecărei neomogenități ulterioare este înregistrată într-un semnal slab reflectat, în funcție de timpul de sosire a undelor reflectate în receptor. Această abordare este numită o teorie a undei Born aproximării sau împrăștiere unică [2, 4, 8]. Cu metoda de sonorizare prin impulsuri ecou, în majoritatea cazurilor această aproximare este utilizată. In caz contrar (DA „/ k“ 1) val nu propagă în interiorul obiectului testat și unda obiect poate fi sesizat pentru a obține informații cu privire la forma frontierei sale, și nu structura internă. Rezoluția sondei, în special a dispozitivelor cu ultrasunete, crește cu frecvența ω. Aici, pentru undele ultrasonice crește odată cu creșterea frecvenței și coeficientul de amortizare la 8 w „[13], care, în principiu, limitează banda spațială a dispozitivelor cu ultrasunete.
În cazul unui mediu ușor neomogen, când dimensiunile neomogenității sunt mult mai mari decât lungimea de undă ((gradk («к.
Fig. 3), semnalul reflectat poate fi practic absent, iar pentru rezolvarea problemelor inverse se folosesc principiile de tomografie de refracție. În astfel de probleme, faza semnalelor de undă de-a lungul razelor (traiectoriilor) propagării valurilor este integrată. Razele sunt în acest caz curbe ale căror forme depind de viteza (indicele de refracție) al mediului. Acest indice de refracție este cantitatea dorită, a cărei distribuție spațială trebuie să fie restabilită. Datele inițiale în astfel de sarcini sunt timp întârzieri semnale (faza) de undă se propagă de-a lungul diferitelor raze sau unghiuri raze de sosire în diferite puncte ale spațiului. Metodele refractari Tomografie pe scara larga in seismologie (pentru investigarea scoarta terestra), fizica atmosferei (pentru a restabili parametrii atmosferice de mare altitudine la lustruirii sale într-o frecvențe optice sau de radio), oceanografia (pentru a restabili profilul densității, salinitate, temperatura din adâncimea oceanelor în termenii sunetului valuri) [3, 15, 19, 21, 22].
Să luăm în considerare două abordări teoretice de bază pentru rezolvarea problemelor de undă inversă.