Din acest articol, veți învăța elementele de bază ale probabilității de poker în Texas Hold'em. Vom analiza toate nuanțele și vom examina toate exemplele. Și începem cu informații generale despre combinații și probabilități.
1. Combinații și probabilități ale mâinilor de buzunar
Numărul de opțiuni pentru mâinile de pornire este 52 x 51/2 = 1326 combinații unice cu costume de cost. De ce suntem împărțiți în două? Deoarece ordinea cărților nu este importantă pentru noi. "5 ♣, 8 ♦" sau "8 ♦, 5 ♣" - pentru noi se consideră aceeași combinație.
Dar dacă te gândești mai adânc, atunci este puțin probabil să fii important pentru tine care este triplele tale de tamburine, viermi, vârfuri sau cluburi? Dacă renunți la semnificația costumului, atunci obținem doar 169 de combinații posibile:
- 13 perechi
- 78 mâini potrivite
- 78 de mâini diferite
Cunoscând aceste numere este ușor de găsit probabilitatea unor evenimente interesante.
1.1. Probabilitatea de a obține o pereche de buzunar
De exemplu, probabilitatea de a obține o pereche este de 13/52 * 12/51 ≈ 5,88%. Cu alte cuvinte, la fiecare mâna a 17-a vom avea o pereche. Cum am obținut numărul 17 pe care îl întrebi? Da, este foarte simplu: trebuie să împărțiți 100% în 5,88%.
1.2. Probabilitatea de a obține o pereche de ași de buzunar
O întrebare interesantă, pentru că o pereche de ași este cea mai bună mână de poker. Numărăm: numai într-un pachet de 52 de cărți - 4 ași. Probabilitatea de a obține un ace 4/52, al doilea as 3/51. Prin urmare, probabilitatea de a obține o pereche de ași este de 4/52 x 3/51 = 0,45%. Cu alte cuvinte, fiecare mâna.
1.3. Probabilitatea de a obține o mână de buzunar de sus
mâini de buzunar de top :. "AA", "KK," QQ "" AK "" AQ "" KQ „Noi credem probabilitatea de: 0,45% + 0,45% + 0,45% + 0.59% + 0.59% + 0.59% ≈ 3,13% sau la fiecare 32 de mâini.
Să rezumăm rezultatul mic și să elaborăm o masă interesantă pentru obținerea mâinilor de buzunar.
1.4. Tabel cu probabilități de primire a mâinilor de buzunar
2. Probabilitatea - modul de numărare
Probabilitatea poate fi văzută din două părți. Prima este probabilitatea de îmbunătățire. A doua este probabilitatea de a câștiga, știind numărul de rivali și cărțile de buzunar.
2.1. Probabilitatea de a se îmbunătăți
Această probabilitate depinde de numărul de outs - cărți care pot îmbunătăți combinația. Cele mai multe ori despre outs sunt vorbite cu o strada neterminata sau flash. De exemplu, cu 8 outs, probabilitatea de îmbunătățire pe turn:
8/47 ≈ 17%.
pe râu:
8/46 ≈ 17,4%
Rețineți că împărțim numărul cărților pe care nu le știm. Probabilitatea de îmbunătățire pe turn sau pe river nu poate fi rezumată! Pentru a găsi probabilitatea de a îmbunătăți împreună și la rândul său și pe râu, trebuie să aplicați calcule speciale în funcție de teoria probabilității.
Pentru a face acest lucru, vom calcula probabilitatea că nu ne vom îmbunătăți nici pe turn sau pe river:
39/47 x 38/46 ≈ 68,5%
Se scade din 100% această probabilitate și se obține: 100% - 68,5% = 31,5%. Aceasta este ≈ 31,5% din faptul că vom putea colecta combinația până la sfârșitul desenului.
2.2. Probabilitatea victoriei
De exemplu, ia în considerare o situație simplă. Sunt 6 jucători la masă (inclusiv pe tine). Ai fost pre-flop cu cărți: "10 ♠, Q ♥". Folosind calculatorul de poker, vom determina probabilitatea victoriei dvs.: 25.170%.
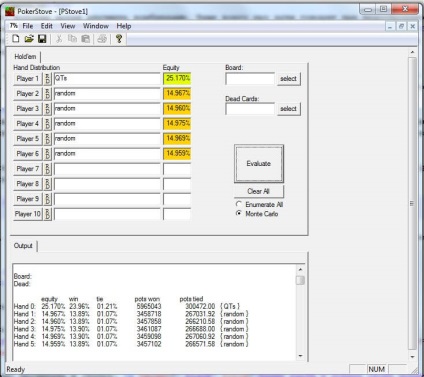
Apoi, pe flop au coborât cărțile: "J ♣, 8 ♦, 4 ♣". Noi conducem în calculator aceste valori și vedem că șansele de victorie au scăzut: 24.335%.
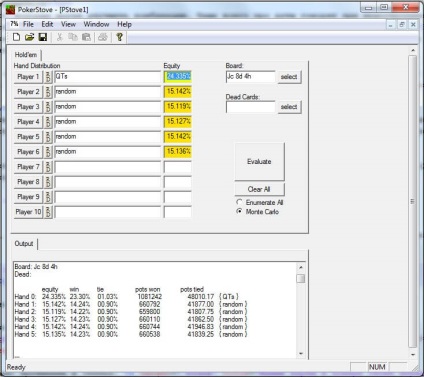
În mod similar, puteți continua să numărați.
Există multe mese gata făcute cu probabilități de victorie împotriva unei mâini arbitrare. De exemplu:
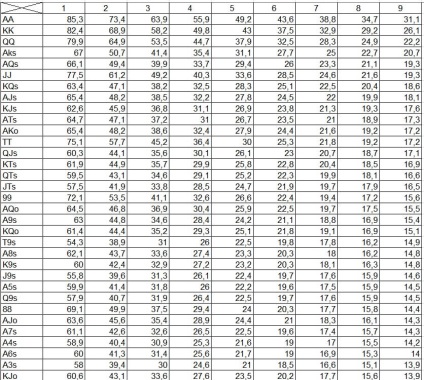
Mai multe detalii despre mâini și mese puternice pot fi citite în articol: ce mâini merită să jucați. precum și descărcați o arhivă cu informații utile despre acest subiect: startovye-ruki.rar
3. Probabilitatea sosirii cardului
Despre acest motiv, pentru vreun motiv, nimeni nu scrie, deși, în opinia mea, contează și el. Faptul este că fiecare distribuție este independentă una de cealaltă, dar există încă o probabilitate. De exemplu, pe bord pentru cinci runde nu au existat ași și regi. Asta este, putem presupune că a șasea distribuție a șanselor de apariție a acestora la bord este destul de mare.
Cum se poate folosi aceasta? Trebuie să vă amintiți despre cardurile care nu au existat mult timp. Și dacă aveți cărți la îndemână (Ace, Rege), atunci este logic să jucați agresiv. La urma urmei, există șanse mari de a obține o pereche în cele din urmă.
Din câte știu, algoritmii pentru numărarea hărților vechi nu au fost încă creați. Prin urmare, rămâne să sperăm pentru memorie. Amintiți-vă că trebuie să se joace doar la o masă, și nu după o grămadă, așa cum mulți ar dori să facă.