Un câmp vectorial se numește solenoid. dacă există un astfel de câmp vectorial. pentru care câmpul este câmpul rotorului :.
Un câmp se numește potențialul vector al unui câmp vectorial.
Semnul solenoidalității unui câmp vector: câmpul vectorial este solenoidal dacă și numai dacă divergența lui este zero. (14)
Decizia unei variante aproximative a WPW
Sarcina 1. Calculați forța forței atunci când deplasați punctul de aplicare a forței de-a lungul unei curbe date L. de la punctul B la punctul C. Dacă valorile parametrului t la punctele B și C sunt date prin :.
Pentru a calcula lucrarea folosim integralele curbiliniare ale celui de-al doilea tip (formula (3)) :.
Parametrul curbilinar redus este redus la un integral integral folosind ecuațiile parametrice ale curbei BC:
Pentru o anumită curbă, obținem:
Astfel, pentru a găsi lucrarea, trebuie să calculam un integral integral:
Facem o schimbare a variabilei într-un integral definitiv:
Folosim metoda "însumării unei părți a integranței sub semnul diferențialului":
A: U. lucru.
Problema 2. Vectorul de radius al punctului de deplasare este specificat:
. Găsiți vectorii de viteză și accelerare din acest punct în 2 minute de la începutul mișcării.
Funcția Vector este dată în formă de coordonate :.
Gasim primul si al doilea derivat al proiectiilor lui x (t), y (t) z (t) in raport cu argumentul t:
Să găsim vectorii de viteză și accelerare a mișcării punctului conform formulelor (4) și (5):
La 2 minute după începutul mișcării, vectorii de viteză și accelerare vor fi:
Problema 3. Se dă un câmp vectorial și ecuația planului d. 3x + y + 2z - 3 = 0. Necesar:
1) găsiți câmpul de curgere prin planul triunghiului ABC unde AV și C - punctul de intersecție a planului cu axele de coordonate d, într-un plan normal direcție orientată „de origine“; construct desen OABC piramidă. în cazul în care G - originea;
2) folosind formula Ostrogradsky-Gauss, calculați fluxul câmpului pe întreaga suprafață a piramidei OABC în direcția exteriorului normal.
1) Pentru a calcula fluxul câmpului prin planul triunghiului ABC, folosim formula (6): SAWS =. unde D este proiecția triunghiului ABC pe planul xOy. F este o funcție care specifică planul d. care aparține triunghiului ABC.
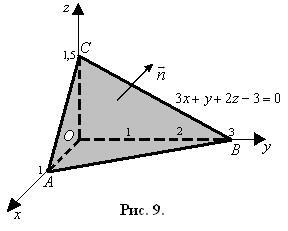
Vom construi desenul piramidal, punem punctele AV AVC pe axele coordonatelor și le vom conecta cu originea O (figura 9).
Din ecuația planului d. 3x + y + 2z - 3 = 0, care are forma F (x, y, z) = 0, găsim.
Deoarece toate cele trei proiecții gradient pozitiv, atunci acest vector axe de coordonate forme cu colțuri ascuțite, și anume regia de la „origine“ la planul d. Aceasta înseamnă că vectorul și vectorul unitate de „străin“ normal. specificate în problema, au aceeași direcție, astfel încât calculul debitului prin planul triunghiului ABC se reduce la un calcul al unui dublu integrală: Paws = + (înainte de setul integrală semnul „+“), în cazul în care AOV - proiecție pe triunghiul ABC xOy avionul.
Pentru a aranja limitele de integrare de-a lungul triunghiului AOB (Figura 10), găsim ecuația liniei AB în planul xOy:
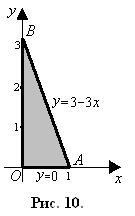
Astfel, fluxul câmpului prin planul triunghiului ABC:
Calculam integralul intern cu privire la variabila y:
Calculam integralul exterior cu privire la variabila x:
2) Pentru a calcula fluxul câmpului pe întreaga suprafață a piramidei OABC. folosim formula Ostrogradsky-Gauss:
Să găsim divergența acestui câmp prin formula (8): Pentru câmp obținem:
Calculam fluxul câmpului prin suprafața completă a piramidei OABC:
. unde este volumul piramidei OABC. Acest volum poate fi calculat după cum urmează:
Ca rezultat, obținem :.
Problema 4. Verificați dacă câmpul vectorial de forță este potențial sau solenoidal. În cazul unui câmp potențial, găsiți potențialul său și calculați forța potențială prin deplasarea masei unității de la punctul M (0,1,0) la punctul N (-1,2,3).
Pentru a verifica potențialul câmpului vectorial, găsim rotorul cu formula (10):
Prin urmare, câmpul este potențial.
Pentru a verifica solenoiditatea câmpului, găsim divergența sa prin formula (8):
În consecință, câmpul nu este solenoidal.
Pentru a găsi un potențial U (x, y, z) de decolare câmp vectorial într-un punct fix (0,0,0), punctul curent C (x, y, z) și calcula linia integrală de-a lungul frântă VEKC. unități care sunt paralele cu axele de coordonate și E (x, 0,0), K (x, y, 0) (vezi. fig. 7). Prin formula (12) obținem:
Am obținut potențialul de teren. unde C este o constantă arbitrară. Pentru a verifica soluția, găsim gradientul potențial. . În consecință, potențialul câmpului de forță este găsit corect.
Să găsim lucrarea unui câmp vectorial atunci când se deplasează masa de unitate de la punctul M (0,1,0) la punctul N (-1,2,3) prin formula (11):
Răspunsuri: câmpul este potențial non-solenoidal; . unde C este o constantă arbitrară; locul de muncă A = -10.